Курсовая работа: Тепломассообмен при испарении и горении капель жидких топлив

2.1 Метод Зельдовича

Для вывода критического воспламенения воспользуемся методом Зельдовича Я.Б. Разделим область r_к < r < r_пл на две зоны: первая прилегает к поверхности приведенной пленки r_в < r < r_пл ; вторая - r_к < r < r_в . Здесь r_в - координата условной границы, на которой происходит воспламенение. Пренебрегая теплом, выделяющимся при химической реакции во второй зоне r_к < r < r_в , уравнение (1.2) запишем в виде

(2.1)

решая которое получим

а с учётом

имеем выражение для теплового потока

(2.2)

Для первой зоны r_в < r < r_пл, пренебрегая изменением температуры с координатой, так какдействие химических источников способствует выравниванию температуры по зоне, получим

(2.3)

Сравнивая (2.1) и (2.3) видим, что на границе двух зон r = r_в должна существовать область ,в которой

(2.4)

т.е. количество тепла, выделяемое за счёт химической реакции , равно теплу, отводимому . Равенство (2.4) представим в виде первого условия Семёнова

Второе условие Семёнова, определяет неустойчивость теплового равновесия

(2.5)

Подставив в (2.4) из (2.2)

(2.6)

Скорость химической реакции зависит от концентрации паров и температуры. Для определения связи концентрации с температурой запишем уравнение диффузии

Учитывая подобие граничных условий для температуры и концентрации, можно доказать, что

.

Скорость химической реакции в случае избытка окислителя определяется кинетическим уравнением первого порядка

(2.7)

и зависит только от температуры.

Используя уравнения Семёнова, (2.4) и (2.5), имеем систему уравнений

(2.8)

(2.9)

из которой надо исключить температуру парогазовой смеси Т_в .

Разделив (2.8) на (2.9), получим уравнение

позволяющее выразить Т_в через температуру среды. Оценка величины даёт малую величину по сравнению с . Поэтому без особой погрешности примем

(2.10)

Из (1.13) имеем ранее полученную формулу для массовой скорости испарения

(2.11)

которая при Nu = 2

. (2.12)

Выполним преобразование Франк-Каменецкого

Подставим в (2.8) и используем (2.10)

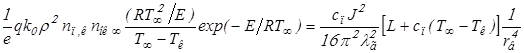
Найдём радиус воспламенения, интегрируя уравнение (2.2) в пределах от r_к до r_в и от r_к до r_пл . В результате получим

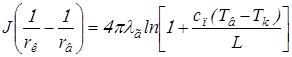
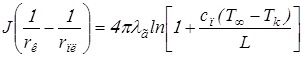
Используя формулу (2.11), имеем

,

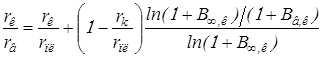где

Учитывая (2.10) и представляя

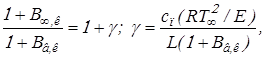
где , получим формулу для r_в в виде

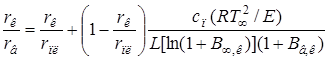(2.13)

Для случая неподвижной среды и координата “поверхности” воспламенения определяется как

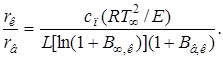
Для капли этилового спирта расчёт по этой формуле даёт r_в /r_к ≈25. Большое расстояние, на котором происходит воспламенение, требует большого времени, чтобы установилось квазистационарное распределение температур и концентраций в газовой фазе. Очевидно, что это время не должно превышать времени полного ис­парения капли. Поэтому критическое условие воспламенения (2.9) совместно с (2.13) для случая неподвижной среды может использоваться только для грубой оценки.