При этом физический смысл const не расшифровывается.

Полагая,что r_к /r_в ≈ r_к /r_пл и используя (2.8), (2.9), (2.10), критическое условие воспламенения капли представим ввиде, аналогичном условию зажигания газовой смеси накаленным телом

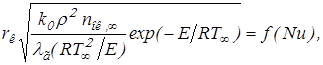(2.15)

где

.

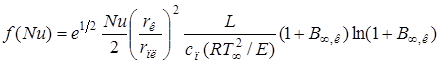
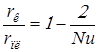2.2 Анализ зависимости критического условия

В отличие от (2.14) в (2.15) содержится информация об испарении. Для жидкости, укоторой величина L/c_п больше, температура воспламенения должна быть при постоянных других свойствах. Наиболее чувствительна температура воспламенения кэнергии активации. Так у ацетона энергия активации больше (Е_ац /Е_сп =1.31) а величина L/c_п меньше чем у этилового спирта (L/c_п )_ац /(L/c_п )_сп = 0.72. В итоге температура воспламенения уацетона выше, чем у этилового спирта, так как величина L/c_п входит под знак логарифма. С увеличением скорости потока температура воспламенения увеличивается , а с ростом радиуса капли уменьшается. Это объясняется тем, что рост скорости потока приводит к увеличению теплоотвода из зоны химической реакции. Увеличение же размеров капли в результате приводит к увеличению мощности тепловыделения. Поэтому воспламенение капли большего диаметра происходит при меньшей температуре газа.

Раздел 3.

гистерезис горения. срыв пламени

3.1. Горение в потоке воздуха.

Горение жидкой поверхности в движущемся воздушном потоке обстоятельно изучалось Сполдингом[2]. Опыты проводились на горелках с рецирку­ляцией, в которых топливо (в большинстве случаев керосин) омывало поверхность горелки и снова собиралось. Использовались горелки с вертикальной плоской пластинкой и сферические горелки (последние воспроизводили каплю жидкого топлива). Изменение расхода топлива позволяло изменять количество тепла, поглощаемого топливом. Размеры горелок были таковы, что приходилось учитывать влияние естественной конвекции. Сполдинг [2] проводил также опыты по горению на шарике при вынужденной конвекции.

Не приводя окончательного вывода, Сполдинг [2] пред­лагает следующее уравнение, выраженное через безразмерные параметры, для горения на вертикальной плоской пластинке при ламинарной естественной

конвекции:

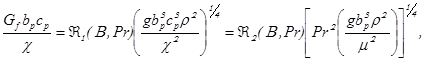(3.1)

где

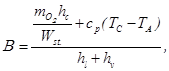
а — вес кислорода на единицу веса газовой смеси в атмосфере.

?? ???????????, ????? ???????? ??????? ????????? ??? ???????? ????????????, ?????????, ???????????? ???????????????? ? ???????????? ????????. ???????? ? ????? ???????? ??????????? ?????????????? ??????? ??? ????????? ???????????. ??????? ????????, ??? ????????? / ???????? ?????? ????? ????????. ??????? ????? ???????? 0,769 ln(1 + ) ??? ?r = 0,71 (??? ???????).

Скорость диффузии от плоской пластинки, обтекаемой в продольном направлении ламинарным потоком в условиях вынужденной конвекции, дается выражением

, (3.2)

При Рr = 0,71 функция апроксимируется выражением 0,646 ln(1 + ).

Установлено, что скорость диффузии (скорость горения) может быть определена приближенно по известным данным о теплопередаче из выражения

, (3.3)

где Н — коэффициент теплопередачи, определяемый экспериментальным путем в отсутствие горения или диффузии.

Уравнение (3.3) напоминает уравнение (8а), которое, будучи написано для скорости горения на единицу поверхности, принимает вид

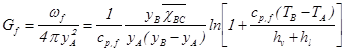, (3.4)

Член можно заменить коэффициентом, теплопередачи.

Если ввести температуру горения из уравнения (34а), то получим

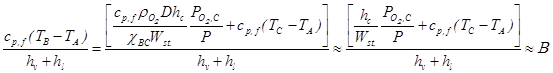, (3.5)

так как с_р р D /х ~ 1 и для воздуха .Таким образом, видна взаимосвязь уравнений (46) и (47).

3.2. Естественная конвекция.

В своих опытах по горению в условиях естественной конвекции Сполдинг применял горелку с плоской пластинкой длиной 63,5 мм и шириной 52,8 мм и сферическую горелку с шариком диаметром 38 мм. При изменении расхода топлива количество поглощаемого жидкостью тепла могло достигать 2220 ккал на 1 кг сжигаемого топлива. Это позволяло изменять Н₀ + Н_г в значительно больших пределах, чем при горении отдельных капель топлив.

Данные как для плоской, так и для сферической горелки хорошо описываются уравнением (3.1). При горении на сфере в качестве характеристического размера использовался ее диаметр, а при горении на пластинке — ее высота. Сполдинг подтверждает правильность такой методики тем обстоятельством, что данные по теплообмену при естественной конвекции на пластинках, шарах и цилиндрах хорошо коррелируются одной зависимостью, так что то же самое может оказаться справедливым и в случае горения. Большинство опытов было проведено по горению керосина, но уравнение (3.1) дает возможность так же хорошо рассчитать данные для газойля, бензина и тяжелых мазутов. Считается, что уравнения (3.1) и (3.3) можно применять и для расчета скорости горения при естественной конвекции.

3.3. Вынужденная конвекция .

В большинстве своих опытов в условиях вынужденной конвекции Сполдинг использовал сферическую горелку диаметром 25,4 мм, а в качестве топлива — керосин, бензин, этиловый спирт и бензол. Скорости горения на плоской пластинке, вычисленные по уравнению (3.2), оказались на 10—3.2% ниже, а вычисленные по уравнению (3.3) —на туже величину выше экспериментальных значений. Воспроизводимость данных хуже, чем данных, полученных при естественной конвекции. Вычисленное по уравнению (3.3) время сгорания капель ракетного топлива диаметром 100 мкм при температуре воздушного потока 205° и скорости капли относительно воздуха 3.2 м/сек составляет 5 мсек. В отсутствие конвекции время сгорания составляет 12 мсек. -

Эммонс произвел более точный расчет для горения на плоской пластинке при вынужденной конвекции, в котором число Рг принималось равным 1. Результаты этого расчета несколько лучше совпадают с экспериментальными данными, чем результаты, полученные по уравнению (3.2) или (3.3).

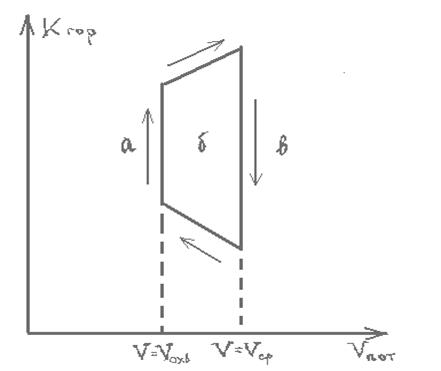
При проведении опытов по горению на сферах в воздушном потоке было обнаружено, что при критической скорости воздуха верхняя половина оболочки пламени, окружающего шарик, гаснет. Сполдинг назвал это явление затухания достижением химического предела скорости горения. С увеличе­нием скорости воздуха пограничный слой становится тоньше, а перенос массы к фронту пламени возрастает. Поскольку скорости химических реакций, протекающих на поверхности горения, конечны, реакционная зона утолщается, и температура ее падает. В конце концов, достигается такое положение, когда скорость химической реакции отстает от скорости подвода топлива и кислорода к зоне горения и пламя гаснет. Сполдинг проводил опыты по затуханию пламени в условиях вынужден­ной конвекции на шариках разного диаметра (7—26 мм). По расчету в момент затухания скорость воздушного потока, вы­раженная числом диаметров в секунду, и расстояние пламени от поверхности шарика на лобовой его части не должны зависеть от диаметра шарика. Это подтвердилось с точностью до 10% при изменении диаметра шарика в 3,7 раза.

Топе использовал другой метод изучения горения в условиях конвекции. В его опытах капли топлива (с первоначальным диаметром 300—600 мкм) падали в нагретую топку при своих предельных скоростях. Таким путем были получены количественные данные по испарению в атмосферах с высокой температурой. По определению остатка при горении капель мазутного топлива представлены лишь немногие качественные данные.

Вообще уравнения Сполдинга дают возможность надежно определить экспериментальные скорости горения при естественной и вынужденной конвекции. Размер капель в струе топлива на 3 или больше порядков меньше, чем размер сферических горелок, использованных Сполдннгом, а других количественных данных по горению в условиях конвекции нет. Поэтому его уравнения нельзя использовать с уверенностью в расчете для случая горения мелких капель.

Литература

1. Калннчак В. В. , Федосеева Н. В. // Химическая физика процессов горения и взры­ва. Горение гетерогенных и газовых систем.—Черноголовка, 1977.