Курсовая работа: Термодинамические основы термоупругости
получим тензорное уравнение
, (1.1.5)
Решая это тензорное уравнение относительно компонентов тензора напряжений, найдем
(1.1.6)
где
(1.1.7)
обозначает расширение тела и
γ = α(3λ + 2μ). (1.1.8)
Физический закон, выраженный тензорным соотношением (1.1.6), называется законом Дюамеля — Неймана
Термодинамическими переменными, описывающими состояние упругого тела, являются компоненты деформации (1.1.2) и абсолютная температура Т +
.
Используя методы термодинамики обратимых процессов, Био показал, что энтропия s единицы объема тела определяется соотношением
(1.1.9)
где аддитивная постоянная, входящая в определение энтропии, была выбрана таким образом, что энтропия была равна нулю в начальном состоянии. В этом уравнении ρ — плотность тела, с — удельная теплоемкость единицы массы (принимаемая независимой от температуры вблизи равновесной температуры T), и γ определяется формулой (1.1.8). Если мало по сравнению с Т то соотношение (1.1.9) сводится к простому выражению для энтропии единицы объема
(1.1.10)
Таким образом, количество тепла, поглощаемое единицей объема в процессе малых деформаций и малых изменении температуры, определяется формулой
h=Ts = ρс+ γTΔ(1.1.11)
Из теории теплопроводности в твердых телах известно, что изменение температуры внутри изотропного тела подчиняется уравнению
(1.1.12)
k— коэффициент теплопроводности тела;
q — количество тепла;
выделяемого в единице объема тела. Подставляя выражение (1.1.10) в соотношение (1.1.11), найдем
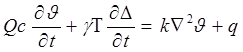(1.1.13)
Если ввести коэффициент температуропроводности
,
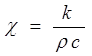то последнее уравнение можно записать в форме
(1.1.14) где
, 
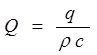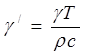
Для того чтобы дополнить систему основных уравнений, присоединим к ней уравнения движения в виде
, (1.1.15)