Курсовая работа: Цифровой сглаживающий фильтр

Введение

С внедрением в промышленность цифровых технологий появилась возможность строить устройства обработки оцифрованных сигналов вычислительным методом. Такой способ обладает рядом важных преимуществ, таких как повышенная точность обработки, меньшая зависимость параметров от внешних условий, а также возможность реализации таких обрабатывающих устройств, которые невозможно или трудно было реализовать в аналоговом виде. К таким устройствам относятся и цифровые фильтры, для которых стало возможным построение разнообразных частотных характеристик путем их аналитической задачи. При этом реализуемы и фильтры традиционных типов: нижних частот, верхних частот, полосовые и режекторные.

Сглаживающий фильтр относится к особому типу фильтров и призван убирать из сигнала импульсные проявления (пики и щелчки), сглаживая их. Импульс имеет широкий (в идеале бесконечный) частотный спектр, однако острота его формы определяется именно высокочастотными составляющими.

По заданию требуется спроектировать цифровой сглаживающий фильтр, используя набор К1821, включающий микропроцессор ВМ85, ПЗУ и порты ввода-вывода на микросхеме РФ55, ОЗУ, таймер счетчик и порты на микросхеме РУ55. Входной сигнал аналоговый, оцифровывается с помощью 10-разрядного АЦП 1108ПВ1, после чего имеет вид отсчетов, следующих через интервал дискретизации. После обработки сигнал в дополнительном цифровом коде должен передаваться в порт ввода-вывода по алгоритму с квитированием. Частота дискретизации F_Д = 5 кГц, разрядность выходного сигнала 8. Обработка должна происходить в реальном масштабе времени. При проектировании следует придерживаться двух критериев: минимальная аппаратная конфигурация устройства и минимальное время операций обработки сигнала (вычисления). При определенных условиях эти критерии противоречат друг другу.

Фильтр есть линейное устройство, производящее операции над частотным спектром исходного сигнала. Для понимания процесса обработки сигнала в цифровом фильтре полезно знать его основные характеристики. Передаточная функция фильтра, определяющая отношение выходного сигнала к входному при конкретном значении комплексной частоты, по заданию имеет вид:

H(z) = 0.4 (0.1 + 0.65z ^–1 + z ^–2 + 0.65z ^–3 + 0.1z ^-4 ) (1),

здесь z = e ^{p T} _д - характеризует задержку отсчета на время, равное интервалу дискретизации Т_Д = 1/F_Д = 0.2 мс. Для данного случая это означает, что амплитуда очередного выходного отсчета равна сумме амплитуд пяти последних входных отсчетов, помноженных на соответствующие коэффициенты. Когда на вход поступает очередной отсчет, по этому правилу сразу вычисляется очередной выходной. По сути это и есть алгоритм работы цифрового фильтра, который требуется спроектировать.

По этому алгоритму, при подаче на вход единственного единичного отсчета фильтр ответит пятью отсчетами, следующими через Т_Д и имеющими амплитуды, равные соответствующим коэффициентам передаточной функции:

Видно, что высокий острый импульс сглаживается и растягивается во времени.

Если на вход подается последовательность из пяти и более единичных отсчетов, то на выходе будет наблюдаться последовательность нарастающих по амплитуде импульсов, причем каждый последующий больше предыдущего на соответствующий коэффициент, а начиная с пятого все отсчеты имеют единичную амплитуду:

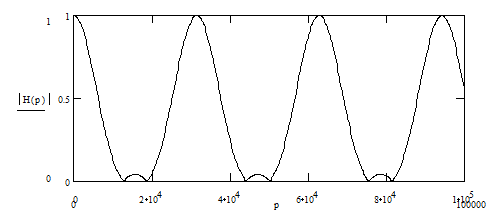
Строго говоря, выражение (1) является аналитическим описанием дискретного режекторного гребенчатого фильтра нерекурсивного типа ( с конечной импульсной характеристикой ).

Гребенчатость фильтра связана со стробоскопическим эффектом при оцифровке сигнала, когда бесконечное множество аналоговых колебаний различных частот имеют одинаковую дискретную реализацию в отсчетах и, следовательно, обрабатываются фильтром одинаково. Но только одно из таких колебаний имеет частоту, меньшую частоты дискретизации, а значит, остальные колебания не отвечают требованию теоремы Котельникова, согласно которой верхняя частота сигнала должна быть как минимум в два раза меньше частоты дискретизации, иначе может произойти потеря информации, закодированной в дискретном сигнале. По заданию, F_Д = 5 кГц , следовательно, верхняя частота сигнала, а значит, и фильтра составляет

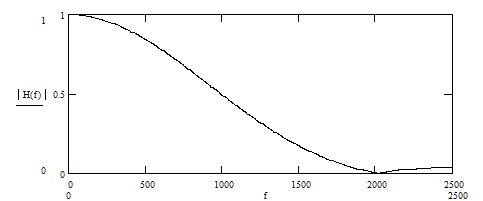
F_В = 2.5 кГц.

1. Анализ и формализация задачи

Согласно техническому заданию и выражению (1), обобщенная структура, описывающая работу фильтра, выглядит следующим образом:

Z-1

Z-1

Z-1

Z-1

x_n

b0

b1

b2

b3

b4

C

S

y_n

где x_n – входные отсчеты, y_n – выходные отсчеты,

z ^–1 – задержка на Т_Д , b_m и С – коэффициенты.

Как видно, фильтр должен держать в памяти пять отсчетов одновременно и оперировать с ними, производя арифметические операции. С выполнением поставленной задачи может справиться микропроцессорная система, действующая по заданной программе. Она составляет основу цифрового фильтра и включает в себя микропроцессор, оперативную память для хранения отсчетов и постоянную память для хранения кода программы, реализующей алгоритм фильтрации. Согласно заданию, микропроцессорная система строится на основе комплекта К1821, включающего микропроцессор ВМ85, микросхему РФ55 ( ПЗУ и порты ввода-вывода ) и микросхему РУ55 (ОЗУ, таймер-счетчик и порты ввода-вывода ).

Исходный сигнал, который фильтр должен обрабатывать, имеет аналоговую форму, поэтому его необходимо оцифровать. Для этой цели используется аналогово-цифровой преобразователь (АЦП) последовательного приближения 1108ПВ1. Данный АЦП работает с униполярным сигналом от 0 до 3 вольт, поэтому необходимо обеспечить масштабирование и сдвиг на +1.5 В аналогового сигнала, который по заданию изменяется в пределах от -2 до +2 В. Это осуществляется с помощью высокостабильного резистивного делителя и развязывающего повторителя, выполненного на операционном усилителе.

АЦП 110ПВ1 – десятиразрядный, данные выдаются в прямом параллельном коде. Вычисление начинается с отрицательным перепадом тактового импульса (ТИ) при условии низкого уровня на входе запуска ST. в течении первого тактового импульса происходит сброс регистров и установка опорных напряжений на входе внутреннего селектора АЦП. Далее в течении 10 ТИ осуществляется последовательное приближение, и в последнем 12-м ТИ формируется низкоуровневый сигнал RAD, служащий для оповещения внешнего устройства о готовности данных ( присутствии их в выходном буфере). АЦП может работать и в 8-разрядном режиме, если его вход SE10/8 подключен к шине отрицательного источника питания, при этом приближение происходит за 8 ТИ и таким образом, на преобразование затрачивается 10 тактов. Следует заметить, что у данного АЦП может быть внешнее или внутреннее тактирование, в последнем случае частота следования тактовых импульсов определяется величиной конденсатора C_CLK , при С_СLK = 10 пФ f_max = 27 МГц, t_min = 37 нс, время преобразования t_пр = 10t_min = 0.37 мкс, отсюда следует, что максимально возможное время обработки микропроцессором данных t_обр = T_Д – t_пр = 200-0.37=199.63 мкс, то есть, время выборки занимает ничтожную часть общего времени Т_Д , отведенного на получение очередного входного отсчета и вычисление выходного.

Однако за малое время t_пр сигнал на входе АЦП может меняться, и в результате приближений выходная информация не будет соответствовать действительности. Необходимо, чтобы во время аналогово-цифрового преобразования уровень входного сигнала был постоянен, или хотя бы не изменялся более чем на 0.5h , где h – шаг квантования

Максимальное изменение будет происходить на верхней частоте, равной согласно теореме Котельникова

f_в = 0.5 F_Д = 2.5 кГц. Скорость этого изменения можно рассчитать, взяв производную от испытательного колебания с частотой f_в и размахом U_{вх max} = 3 B.

S(t) = 3 sin (2p * 2500 t ); S’(t) = 3*2p *2500 cos (2p *2500 t );

Максимальная скорость изменения равна 3*2p*2500 » 47124 В/с.

Du = 47124 * 3.7*10^-7 = 17.4 мВ > 5.86 = 0.5h.

Чтобы поддерживать сигнал на входе АЦП постоянным на время преобразования, требуется устройство выборки и хранения (УВХ), которое фиксирует уровень с момента прихода на управляющий вход тактирующего строба и удерживает этот уровень в течении всей его длительности. В простейшем случае УВХ представляет собой аналоговый ключ и емкость хранения:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--