Курсовая работа: Циклоида
Это построение — чисто геометрическое, хотя получили мы его, используя понятия механики. Теперь мы можем проститься с механикой и дальнейшие следствия получать без ее помощи. Начнем с простой теоремы.
Теорема 1. Угол между касательной к циклоиде (в произвольной точке) и направляющей прямой равен дополнению до 90° половины угла поворота радиуса производящего круга.
Иными словами, на нашем рис. 17 уголKLT равен ![]() или
или
∟КМР = ![]() .
.
Это равенство мы теперь докажем. Для сокращения речи условимся угол ![]() поворота радиуса производящего круга называть «основным углом». Значит, угол МОТ на рис. 17 — основной угол. Будем считать основной угол острым. Читатель сам видоизменит рассуждения для случая тупого угла, т. е. для случая, когда катящийся круг сделает больше четверти полного оборота.
поворота радиуса производящего круга называть «основным углом». Значит, угол МОТ на рис. 17 — основной угол. Будем считать основной угол острым. Читатель сам видоизменит рассуждения для случая тупого угла, т. е. для случая, когда катящийся круг сделает больше четверти полного оборота.
Рассмотрим угол СМР. Сторона СМ перпендикулярна к ОМ (касательная к окружности перпендикулярна к радиусу). Сторона MP (горизонталь) перпендикулярна к ОТ (к вертикали). Но угол МОГ, по условию, острый (мы условились рассматривать первую четверть оборота), а угол СМР — тупой (почему?). Значит, углы МОТ и СМР составляют в сумме 180° (углы со взаимно перпендикулярными сторонами, из которых один острый, а другой — тупой).
Итак, угол CMP равен 180° — φ Но, как известно, диагональ ромба делит угол при вершине пополам.
Следовательно, угол КМР=90° — ![]() что и требовалось доказать.
что и требовалось доказать.
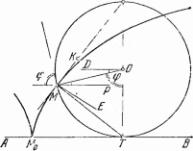
Обратим теперь внимание на нормаль к циклоиде. Мы говорили уже, что нормалью к кривой называется перпендикуляр к касательной, проведенный в точке касания (рис. 16). Изобразим левую часть рис. 17 крупнее, причем проведем нормальME (ME ┴ МК; см. рис. 18).
Из рис. 18 следует, что угол ЕМР равен разности углов КМЕ и КМР, т. е. равен 90° — ∟KMP.
К теореме 2
Но мы только что доказали, что сам угол КМР равен 90° - ![]()
Таким образом, получаем:
∟РМЕ = 90° - ∟ КМР = 90° - (90° - ![]() ) =
) = ![]()
Мы доказали простую, но полезную теорему. Дадим ее формулировку:
Теорема 2. Угол между нормалью к циклоиде (в любой ее точке) и направляющей прямой равен половине «основного угла».
(Вспомним, что «основным углом» называется угол поворота радиуса катящегося круга )
Соединим теперь точку М («текущую» точку циклоиды) с «нижней» точкой (Т) производящего круга (с точкой касания производящего круга и направляющей прямой — см. рис. 18). Треугольник МОТ, очевидно, равнобедренный (ОМ и ОТ — радиусы производящего круга). Сумма углов при основании этого треугольника равна 180° —![]() , а каждый из углов при основании — половике этой суммы. Итак,
, а каждый из углов при основании — половике этой суммы. Итак,
∟OMT = 90°— ![]() .
.
Обратим внимание на угол РМТ. Он равен разности углов ОМТ и ОМР. Мы видели сейчас, что ∟OMT равен 90°- ![]() ; что касается угла ОМР, то нетрудно выяснить, чему он равен. Ведь угол ОМР равен углуDOM (внутренние накрест лежащие углы при параллельных).
; что касается угла ОМР, то нетрудно выяснить, чему он равен. Ведь угол ОМР равен углуDOM (внутренние накрест лежащие углы при параллельных).
 |
3. Основные свойства касательной и нормали к циклоиде
Непосредственно очевидно, что ∟DOM равен 90° — φ.
Значит, ∟OMP = 90° — φ. Таким образом, получаем:
∟РМТ = ∟ОМТ - ∟ ОМР = 90° — ![]() — (90° — φ) =
— (90° — φ) = ![]() .
.
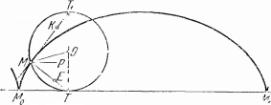
Получается замечательный результат: угол РМТ оказывается равным углу РМЕ (см. теорему 2). Следовательно, прямые ME и МТ сольются! Наш рис. 18 сделан не совсем правильно! Правильное расположение линий дано на рис. 19.
Сформулируем полученный результат виде теоремы 3.
Теорема 3 (первое основное свойство циклоиды). Нормаль к циклоиде проходит через «нижнюю» точку производящего круга.
Из этой теоремы получается простое следствие. Угол между касательной и нормалью, по определению, — прямой. Это угол, вписанный в окружность производящего круга. Поэтому он должен опираться на диаметр круга. Итак, ТТ1 — диаметр, и T1 — «верхняя» точка производящего круга. Сформулируем полученный результат.
Следствие (второе основное свойство циклоиды). Касательная к циклоиде проходит через «верхнюю» точку производящего круга.
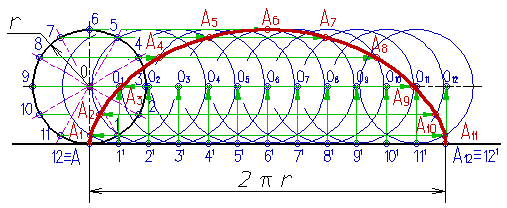
Что бы объяснить это свойство нам необходимо построить циклоиду.
Построение циклоиды.