Курсовая работа: Циклоида

Следствие. Пусть AB задана параметрически

L_AB = (1)

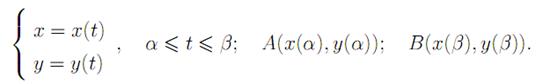
Пусть функции x(t), y(t) непрерывно-дифференцируемые на [α, β]. Тогда

формулу (1) можно записать так

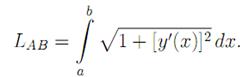
Сделаем замену переменных в этом интеграле x = x(t), тогда y’(x)= ;

dx= x’(t)dt и, следовательно:

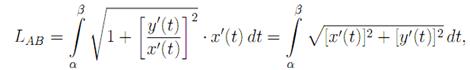
То есть:

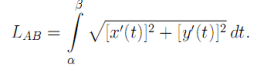
А теперь вернемся к решении нашей задачи.

Решение . Имеем , а поэтому

= 8a

Задача №3. Надо найти площадь поверхности S, образованной от вращения одной арки циклоиды

L={(x,y): x=a(t – sin t), y=a(1 – cost), 0≤ t ≤ 2π}

В интегральном исчислении существует следующая формула для нахождения площади поверхности тела вращения вокруг оси х кривой, заданной на отрезке [a,b] параметрически: x=φ(t), y=ψ(t) (t₀ ≤t ≤t₁ )

|S|=

Применяя эту формулу для нашего уравнения циклоиды получаем:

Задача №4. Найти объем тела, полученного при вращении арки циклоиды

Вдоль оси Ох.

В интегральном исчислении при изучении объемов есть следующее замечание:

Если кривая, ограничивающая криволинейную трапецию задана параметрическими уравнениями и функции в этих уравнениях удовлетворяют условиям теоремы о замене переменной в определенном интеграле, то объем тела вращения трапеции вокруг оси Ох, будет вычисляться по формуле

Воспользуемся этой формулой для нахождения нужного нам объема.

Задача решена.

Заключение

Итак, в ходе выполнения данной работы были выяснены основные свойства циклоиды. Так же научились строить циклоиду, выяснила геометрический смысл циклоиды. Как оказалось циклоида имеет огромное практическое применение не только в математике, но и в технологических расчетах, в физике. Но у циклоиды есть и другие заслуги. Ею пользовались ученые XVII века при разработке приемов исследования кривых линий, — тех приемов, которые привели в конце концов к изобретению дифференциального и интегрального исчислений. Она же была одним из «пробных камней», на которых Ньютон, Лейбниц и их первые исследователи испытывали силу новых мощных математических методов. Наконец, задача о брахистохроне привела к изобретению вариационного исчисления, столь нужного физикам сегодняшнего дня. Таким образом, циклоида оказалась неразрывно связанной с одним из самых интересных периодов в истории математики.

Литература

1. Берман Г.Н. Циклоида. – М., 1980

2. Веров С.Г. Брахистохрона, или еще одна тайна циклоиды // Квант. – 1975. - №5

3. Веров С.Г. Тайны циклоиды// Квант. – 1975. - №8.

4. Гаврилова Р.М., Говорухина А.А., Карташева Л.В., Костецкая Г.С.,Радченко Т.Н. Приложения определенного интеграла. Методические указания и индивидуальные задания для студентов 1 курса физического факультета. — Ростов н/Д: УПЛ РГУ, 1994.

5. Гиндикин С.Г. Звездный век циклоиды // Квант. – 1985. - №6.