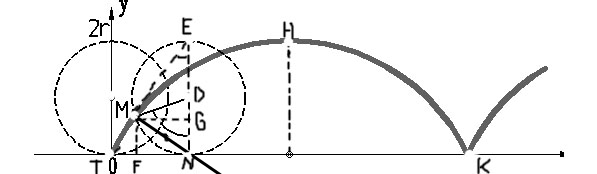
Курсовая работа: Циклоида
y= FM = NG = ND – GD = a – a cos t
Итак параметрические уравнения циклоиды имеют вид:
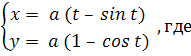 (0
(0
≤ t ≤ 2π).
При изменении t от -∞ до +∞ получится кривая, состоящая из бесчисленного множества таких ветвей, какая изображена на данном рисунке.
Так же, помимо параметрического уравнения циклоиды, существует и ее уравнение в декартовых координатах:
![]() , где r – радиус окружности, образующей циклоиду.
, где r – радиус окружности, образующей циклоиду.
6. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой
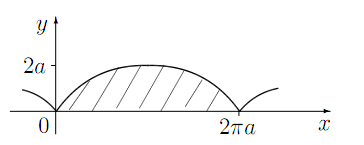
Задача №1 . Найти площадь фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрически
![]()
и осью Ох.
Решение. Для решения данной задачи, воспользуемся известными нам фактами из теории интегралов, а именно:
Площадь криволинейного сектора.
Рассмотрим некоторую функцию r = r(ϕ), определенную на [α, β].
Будем считать, что r и ϕ — полярные координаты точки. Тогда любому
ϕ0 ∈ [α, β] соответствует r0 = r(ϕ0 ) и, значит, точка M0 (ϕ0 , r0 ), где ϕ0 ,
r0 — полярные координаты точки. Если ϕ будет меняться, «пробегая» весь[α, β], то переменная точка M опишет некоторую кривую AB, заданную
уравнением r = r(ϕ).
Определение 7.4. Криволинейным сектором называется фигура, ограниченная двумя лучами ϕ = α, ϕ = β и кривой AB, заданной в полярных
координатах уравнением r = r(ϕ), α ≤ ϕ ≤ β.
Справедлива следующая
Теорема. Если функция r(ϕ) > 0 и непрерывна на [α, β], то площадь
криволинейного сектора вычисляется по формуле:
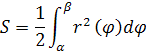
Эта теорема была доказана ранее в теме определенного интеграла.
Исходя из приведенной выше теоремы, наша задача о нахождении площади фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрические x= a (t – sint) , y= a (1 – cost) , и осью Ох, сводится к следующему решению.
Решение . Из уравнения кривой dx = a(1−cos t) dt. Первая арка циклоиды соответствует изменению параметра t от 0 до 2π. Следовательно,
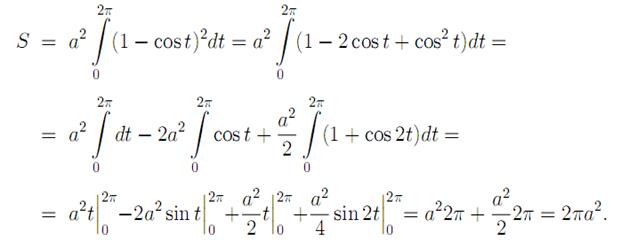
Задача №2. Найти длину одной арки циклоиды
![]()
Так же в интегральном исчислении изучалась следующая теорема и следствие из нее.