Курсовая работа: Управление запасами как элементом оборотных активов

DC в правой части уравнения представляет собой стоимость закупки годовой потребности материала; (D/Q)S — годовые затраты на размещение заказов (фактическое количество размешенных заказов D/Q, умноженное на затраты на размещение одного заказа S), а (Q/2)H — годовые издержки хранения (средний запас Q/2, умноженный на годовые издержки хранения одного изделия H).

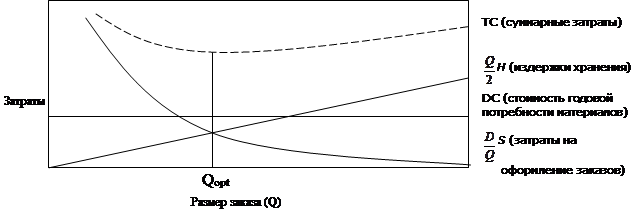
Рис. 2.2 – Зависимости различных составляющих затрат на создание запасов от размера заказа

Затем для разработки модели управления запасами необходимо определить ту величину заказа Q_{opt ,} при которой суммарные затраты минимальны. На рис. 2.2 суммарные затраты достигают минимума в точке, где тангенс угла наклона кривой суммарных годовых затрат равен нулю. Для нахождения точки минимальных затрат возьмем про­изводную от суммарных годовых затрат по Q и приравня­ем ее к нулю. Для рассматриваемого здесь уравнения эти преобразования будут иметь следующий вид [13]:

TC = DC+S+H;

=0+ +=0;

Q_opt =. (2.4)

Поскольку эта простая модель предполагает, что потребность и время выполнения заказа являются постоянными величинами, резервный (буферный) запас не требуется, и точка повторного заказа, R, определяется как:

R=d_av *L, (2.5)

гдеd_av — средняя дневная потребность в материале (постоянная величина);

L— время выполнения заказа в днях (постоянная величина).

2.3.2 Использование модели с фиксированным периодом

В системе управления запасами с фиксированным периодом запас подсчитывается только в определенные моменты времени, например раз в неделю или раз в месяц. Подсчет величины запаса и размещение заказов на периодической основе желательны в ситуациях, когда поставщики с определенной периодичностью навешают своих потребителей и принимают у них заказы на полную номенклатуру своей продукции либо когда покупатели пытаются комбинировать (объединять) заказы для экономии транспортных расходов. Многие фирмы предпочитают модель управления запасами с фиксированным периодом времени, поскольку она облегчает задачу планирования и учета запасов.

Модели с фиксированным периодом времени выдают размеры заказов, разные для различных циклов (в зависимости от нормы потребления). Это, вообще говоря, требует более высокого уровня резервного запаса, чем в системес фиксированным объемом заказа. Система с фиксированным объемом заказа предполагает непрерывный подсчет наличногозапаса, причем заказразмешается сразу же по достижении точки очередного заказа. В отличие от таких систем, в моделях с фиксированным периодом предполагают, что запас подсчитывается только в так называемые контрольные моменты времени. При этом возможно, что исключительно высокое потребление сведет весь запас к нулю сразу же после того, как заказ будет выполнен, и эта ситуация может оставаться незамеченной вплоть до наступления следующего контрольного момента. В таком случае можно оказаться без запаса изделий до поступления очередной партии заказанных изделий (т.е. в течение практически всего контрольного периода Т, плюс время выполнения заказа L ). Таким образом, резервный запас должен защищать нас от дефицита изделий не только в течение контрольного периода, но и в течение времени выполнения заказа — с момента размещения заказа до момента получения изделий по этому заказу.

В системе с фиксированным периодом очередные заказы размешаются в контрольные моменты через время Т, а резервный запас, который необходимо иметь, равен zs_{T + L} .В этом случае потребность характеризуется случайным распределением со средним значением d_av [13]:

Q=d_av (T+L)+zs_T+L -I, (2.6)

где q — размер очередного заказа;

Т -число дней между контрольными моментами;

L — время выполнения заказа в днях (с момента размещения заказа до момента получения изделий по этому заказу);

d_av — прогнозируемая средняя дневная потребность;

z — число стандартных отклонений для заданного уровня обслуживания;

s_{T + L} — стандартное отклонение потребности в течение контрольного периода и периода выполнения заказа;

I— текущий уровень запаса (включает уже имеющиеся изделия).

Величину z можно получить по Е(z), которое определяется по формуле:

E(z)=d_av *Т(1-Р)/s_{T + L} ,(2.7)

где E(z) ― ожидаемая величина дефицита изделий;

Р— требуемый уровень обслуживания, выраженный долей единицы;

d_av — средняя дневная потребность;

Т— количество дней;

s_{T + L} — стандартное отклонение потребности в течение контрольного периода и периода выполнения заказа.

2.3.3 Специальные модели управления запасами

Рассмотренные модель с фиксированным объемом за­каза и модель с фиксированным периодом времени, основанные на равных исходных посылках, все же имеют две общие характеристики — стоимость изделий остается постоянной при любом объеме заказа; процесс очеред­ного размещение заказа предсказуем, т.е. изделия заказы­вались и помешались в запас в расчете на то, что потреб­ность сохранится.

В этом разделе будут представлены две другие модели. Первая иллюстрирует изменение величины заказа в слу­чае, когда цена единицы изделия меняется в зависимости от объема заказа. Вторая, называемая однопериодной моде­лью, или иногда статической моделью, представляет собой задачу, в которой определение размера заказа при каждой закупке требует поиска компромиссного варианта. Для этой модели решение отыскивается на основе анализа предельных показателей.

Модель со ступенчатой (переменной) ценой учитывает то, что в действительности отпускная цена из­делия зависит от объема заказа, причем зависимость цены от размера закупки обычно не прямо пропорциональная, а ступенчатая. Оптимальный объем заказа определяют по наимень­шим общим затратам на создание запасовдля всех значе­ний ЕOQ и Q при которых происходит скачок цены.Для этого составляется таблица, в которой для всех возмож­ных значении объема заказа (все EOQ и размеры закупок Q, при которых установлен скачок цены) рассчитывают все элементы затрат на создание запаса и находят общие затраты на создание запасов. По минимуму общих затрат определяется оптимальный объем закупки. При этом нужно учитывать, что не все значения EOQ имеют смысл, так как могут находиться в диапазонах цен, отличных от тех, по которым они рассчитаны.

Один из практических выполов для моделей со ступен­чатыми ценами состоит и том, что ценовые скидки для крупных закупок часто делают экономически оправданным заказ изделий в количествах, превышающих Q_opt . Таким об­разом, применяя данную модель, мы должны особенно тщательно следить за тем, чтобы получить правильный вы­бор с учетом увеличения потерь от устаревания продукции и затрат, связанных со складированием и хранением. На рисунке 2.3 показана зависимость суммарных затрат на создание запасов в ситуации с тремя уровнями цен.