Курсовая работа: Уравнения равновесия

Содержание

Введение 3

Постановка задачи 4

Уравнения равновесия 5

Решение уравнений равновесия 12

Заключение 16

Список использованной литературы 17

Введение

Актуальным направлением научно-технического прогресса является развитие и широкое использование возможностей современных высокопроизводительных компьютеров, сетей мультипрограммных ЭВМ и на этой основе - применение математических методов моделирования в научных исследованиях. Развитие вычислительной техники в Республике Беларусь приводит к необходимости создания систем и сетей ЭВМ, эффективно обслуживающих запросы различных пользователей. Благодоря задачам, связанным с математическим моделированием мультипрограммных вычислительных систем и анализом их производительности, с проектированием и анализом сетей передачи данных и сетей ЭВМ теория сетей массового обслуживания (СМО) является сравнительно новым и быстро развивающимся разделом теории массового обслуживания.

Исходным материалом для аналитического исследования СМО является стационарное (инвариантное) распределение вероятностей состояний. Ввиду сложности и многомерности случайных процессов, описывающих функционирование таких сетей, большинство аналитических результатов связано с получением стационарного распределения в форме произведения множителей, характеризующих стационарное распределение отдельных узлов сети.

Актуальным вопросом, связанным с исследованием СМО является доказательство инвариатности стационарного распределения таких сетей относительно функционального вида распределений длительности обслуживания в узлах, позволяющее при проектировании и эксплуатации реальных сетей, считать, что обслуживание в узлах имеет наиболее простое для анализа распределение - экспоненциальное.

Постановка задачи

Сеть состоит из двух приборов, на каждый из которых поступает простейший поток с параметрами и соответственно. В случае, если прибор занят, заявка, поступающая на него выбивает заявку находящуюся на приборе, и та становится в очередь на дообслуживание. После обслуживания на I приборе заявка с вероятностью уходит из сети, а с вероятностью поступает на II прибор. Аналогично, после обслуживания на II приборе заявка с вероятностью уходит из сети, а с вероятностью поступает на I прибор.

Пусть - число заявок в очереди на I приборе, - число заявок в очереди на II приборе, - функция распределения времени обслуживания -ой заявки на I приборе, - функция распределения времени обслуживания -ой заявки на II приборе. Предполагается, что

=

=

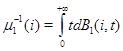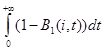
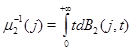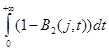
Требуется доказать, что стационарное распределение не зависит от вида функций распределения времени обслуживания . При этом можно считать, что

,

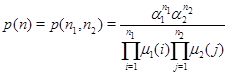где

, ,

т.е. когда - экспоненциальны.

Уравнения равновесия

Введем случайный процесс

,

где - число заявок в очереди на I приборе в момент времени , - число заявок в очереди на II приборе в момент времени , -время, которое еще будет дообслуживаться заявка с момента , стоящая i-ой в очереди I прибора, -время, которое еще будет дообслуживаться заявка с момента , стоящая j-ой в очереди II прибора.

Пусть существует стационарное эргодическое распределение процесса и процесса , т.к. процесс - это процесс , дополненный непрерывными компонентами до того, чтобы быть марковским.

Изучим поведение процесса в устойчивом режиме. Пусть

Введем в рассмотрение событие А, состоящее в том, что

а) Предположим, что за время от до не было поступления требований. Тому, чтобы не изменило за время своего значения и при этом выполнилось событие А, отвечает выражение:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--