Курсовая работа: Устойчивость систем дифференциальных уравнений
Курсовая работа по дисциплине "Специальные разделы математики"
Выполнил студент Новичков А. А., группа: 450
Севмашвтуз - Филиал СПбГМТУ
Кафедра №2
Введение.
Решения большинства дифференциальных уравнений и их систем не выражаются через элементарные функции, и в этих случаях при решении конкретных уравнений применяются приближенные методы интегрирования. Вместе тем часто бывает необходимо знать не конкретные численные решения, а особенности решений: поведение отдельных решений при изменении параметров систем, взаимное поведение решений при различных начальных данных, является ли решение периодическим, как меняется общее поведение системы при изменении параметров. Все эти вопросы изучает качественная теория дифференциальных уравнений.
Одним из основных вопросов этой теории является вопрос об устойчивости решения, или движения системы, если ее трактовать как модель физической системы. Здесь важнейшим является выяснение взаимного поведения отдельных решений, незначительно отличающихся начальными условиями, то есть будут ли малые изменения начальных условий вызывать малые же изменения решений. Этот вопрос был подробно исследован А. М. Ляпуновым.
Основу теории Ляпунова составляет выяснение поведения решений при асимптотическом стремлении расстояния между решениями к нулю. В данной курсовой работе излагаются основы теории Ляпунова устойчивости непрерывных гладких решений систем дифференциальных уравнений первого порядка, а именно: в главе 1 излагаются основные определения, необходимые для изучения устойчивости; в главе 2 дается понятие устойчивости решений систем в общем виде и по первому приближению; в главе 3 излагаются основы второго метода Ляпунова.
1. Свойства систем дифференциальных уравнений.
1.1. Основные определения.
Пусть ![]() — непрерывные в области G (n+1)-мерного пространства скалярные функции.
— непрерывные в области G (n+1)-мерного пространства скалярные функции.
Определение. Совокупность уравнений
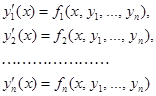 (1)
(1)
называется нормальной системой n дифференциальных уравнений первого порядка. Ее можно записать в матричной форме, если положить
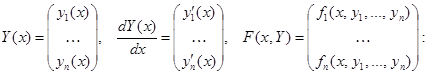
![]()
Определение. Решением системы (1) на интервале (a, b) называется совокупность n функций ![]() , непрерывно дифференцируемых на этом интервале, если при всех
, непрерывно дифференцируемых на этом интервале, если при всех ![]() :
:
![]() ;
;
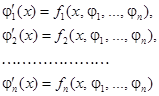
Задача Коши для системы (1) ставится следующим образом: найти решение ![]() системы, определенное в окрестности точки
системы, определенное в окрестности точки ![]() , которое удовлетворяет начальным условиям
, которое удовлетворяет начальным условиям ![]() …,
…, ![]() , где
, где ![]() — заданная точка из области G. Решение задачи Коши существует и единственно, если все функции в правых частях уравнений системы (1) непрерывно дифференцируемы по всем
— заданная точка из области G. Решение задачи Коши существует и единственно, если все функции в правых частях уравнений системы (1) непрерывно дифференцируемы по всем ![]() в окрестности точки
в окрестности точки ![]() .
.
Каждому решению системы (1) сопоставляется 2 геометрических объекта: интегральная кривая и траектория.
Определение. Если ![]() — решение системы (1) на промежутке (a, b), то множество точек (x,
— решение системы (1) на промежутке (a, b), то множество точек (x, ![]() ),
), ![]() , (n+1)-мерного пространства называется интегральной кривой решения, а множество точек (
, (n+1)-мерного пространства называется интегральной кривой решения, а множество точек (![]() ),
), ![]() , n-мерного пространства называется траекторией решения. Заметим, что из существования и единственности решения задачи Коши интегральные кривые не могут пересекаться или иметь общих точек, однако траектории могут пересекаться без нарушения единственности, так как начальная точка определяется n+1 координатой. В частности траектория может совпадать с точкой (положение равновесия).
, n-мерного пространства называется траекторией решения. Заметим, что из существования и единственности решения задачи Коши интегральные кривые не могут пересекаться или иметь общих точек, однако траектории могут пересекаться без нарушения единственности, так как начальная точка определяется n+1 координатой. В частности траектория может совпадать с точкой (положение равновесия).
Система (1) называется автономной, если в правые части уравнений не входит явно независимая переменная. Система (1) называется линейной, если она имеет вид:
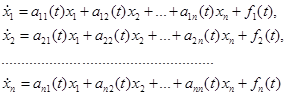 ,
,
или в матричной форме ![]() (1')
(1')
где ![]()
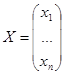 ,
, 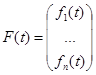 .
.
Фундаментальной матрицей линейной однородной системы называется матричная функция (t), определитель которой отличен от нуля и столбцы которой являются решениями системы: ![]() . С помощью фундаментальной матрицы (t) общее решение системы можно записать в виде
. С помощью фундаментальной матрицы (t) общее решение системы можно записать в виде ![]() . Фундаментальная матрица, обладающая свойством
. Фундаментальная матрица, обладающая свойством ![]() , называется нормированной при
, называется нормированной при ![]() . Если
. Если ![]() — нормированная при
— нормированная при ![]() фундаментальная матрица, то частное решение системы записывается в виде
фундаментальная матрица, то частное решение системы записывается в виде ![]() , где
, где ![]() — начальное при
— начальное при ![]() значение решения.
значение решения.
1.2. Траектории автономных систем.
Будем рассматривать автономную систему в векторной форме:![]() (2)
(2)
где функция f(x) определена в ![]() .
.
Автономные системы обладают тем свойством, что если ![]() — решение уравнения (2), то
— решение уравнения (2), то ![]() ,
, ![]() , также решение уравнения (2). Отсюда в частности следует, что решение
, также решение уравнения (2). Отсюда в частности следует, что решение ![]() можно записать в виде
можно записать в виде ![]() . В геометрической интерпретации эта запись означает, что если две траектории уравнения (2) имеют общую точку, то они совпадают. При этом можно заметить, что траектория вполне определяется начальной точкой
. В геометрической интерпретации эта запись означает, что если две траектории уравнения (2) имеют общую точку, то они совпадают. При этом можно заметить, что траектория вполне определяется начальной точкой ![]() , поэтому можно везде считать
, поэтому можно везде считать ![]() .
.
Пусть ![]() — положение равновесия, т. е.
— положение равновесия, т. е. ![]() . Для того чтобы точка
. Для того чтобы точка ![]() была положением равновесия, необходимо и достаточно, чтобы
была положением равновесия, необходимо и достаточно, чтобы ![]() . Предположим теперь, что траектория решения
. Предположим теперь, что траектория решения ![]() не является положением равновесия, но имеет кратную точку, т. е. существуют
не является положением равновесия, но имеет кратную точку, т. е. существуют ![]() , такие, что
, такие, что ![]() . Так как
. Так как ![]() — не положение равновесия, то
— не положение равновесия, то ![]() . Поэтому можно считать, что
. Поэтому можно считать, что ![]() при
при ![]() . Обозначим
. Обозначим ![]() и покажем, что
и покажем, что ![]() — -периодическая функция.
— -периодическая функция.
Действительно, функция ![]() является решением уравнения (2) при
является решением уравнения (2) при ![]() , причем
, причем ![]() . В силу единственности
. В силу единственности ![]() и
и ![]() совпадают при всех
совпадают при всех ![]() . Применяя аналогичное рассуждение к решению
. Применяя аналогичное рассуждение к решению ![]() , получим, что
, получим, что ![]() определено при
определено при ![]() и функции
и функции ![]() и
и ![]() совпадают при этих t. Таким образом, можно продолжить
совпадают при этих t. Таким образом, можно продолжить ![]() на все
на все ![]() , при этом должно выполняться тождество
, при этом должно выполняться тождество
![]() ,
,
то есть ![]() — периодическая функция с наименьшим периодом.
— периодическая функция с наименьшим периодом.
Траектория такого решения является замкнутой кривой. Из приведенного вытекает следующий результат: Каждая траектория автономного уравнения (2) принадлежит одному из следующих трех типов:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--