Курсовая работа: Властивості рідини і газу

Із законів Ньютона можна показати, що при русі в порожньому просторі імпульс зберігається в часі, а при наявності взаємодії швидкість його зміни визначається сумою прикладених сил. У класичній механіці закон збереження імпульсу звичайно виводиться як наслідок законів Ньютона. Однак, цей закон збереження вірний і у випадках, коли Ньютоновская механіка незастосовна (релятивістська фізика, квантова механіка). Як відзначалося, він може бути отриманий як наслідок інтуїтивно-вірного твердження про те, що властивості нашого миру не зміняться, якщо всі його об'єкти (або початок відліку!) перемістити на деякий вектор L. У цей час не існує яких-небудь експериментальних фактів, що свідчать про невиконання закону збереження імпульсу.

Закон збереження моменту імпульсу.

Якщо поняття імпульсу в класичній механіці характеризує поступальний рух тіл, момент імпульсу вводиться для характеристики обертання і є наслідком твердження про те, що властивості навколишнього світу не змінюються при поворотах (або повороті системи відліку) у просторі.

У випадку нерівності нулю моменту сили спостерігається досить "незвичайне" з погляду "здорового глузду" поводження швидко обертових тіл (їхній момент імпульсу спрямований по осі обертання) з поміщеної на вістря віссю обертання. Такі тіла під дією зовнішніх сил (наприклад, сили ваги) замість того, щоб переміщатися убік дії сили, починають повільно обертатися навколо вістря в перпендикулярній прикладеній силі площини. Незважаючи на те, що подібне поводження є безпосереднім наслідком законів Ньютона (або ще більш загальних законів збереження й симетрії), цей ефект часто не тільки викликає подив в осіб, мало знайомих з точними науками, але й дає їм привід міркувати про "помилковість сучасного природознавства взагалі й класичної фізики зокрема. Заснований на принципі "...якщо я не розумію теорії або спостережуваний ефект, те тим гірше для них...", на жаль дотепер усе ще популярний, хоча вже протягом декількох сторіч природознавство, що розвивається, демонструє його досить низьку евристичну ефективність.

Закон збереження енергії.

Спочатку в механіку були уведені кінетична енергія (обумовлена рухом тіла) і потенційна (обумовленими взаємодіями між тілами й залежна від їхнього розташування в просторі). Конкретне математичне вираження для потенційної енергії визначається взаємодіями між об'єктами. У більшості механічних систем механічна енергія (сума кінетичної і потенційної) зберігається в часі (наприклад у випадку м'яча, що пружно вдаряється об підлогу). Однак нерідкі й такі системи, у яких механічна енергія змінюється (найчастіше убуває). Для опису цього були уведені дисипативні сили (наприклад сили грузлого й сухого тертя й ін.). Згодом з'ясувалося, що дисипативні сили описують не зникнення або виникнення механічної енергії, а переходи її в інші форми (теплову, електромагнітну, енергію зв'язку й т.д.). Історія розвитку природознавства знає кілька прикладів того, як гадане порушення закону збереження енергії стимулювало пошук раніше невідомих каналів її перетворення, що в результаті приводило до відкриття її нових форм (так, наприклад, "безповоротна" втрата енергії в деяких реакціях за участю елементарних часток послужила вказівкою на існування ще однієї невідомої раніше елементарної частки, що згодом одержала назву нейтрино).

Закон збереження енергії має велике практичне значення, оскільки істотно обмежує число можливих каналів еволюції системи без її детального аналізу. Так на підставі цього закону виявляється можливим апріорно відкинути будь-який досить проект досить економічно привабливого вічного двигуна першого роду (пристрою, здатного робити роботу, що перевершує необхідні для його функціонування витрати енергії).

В основі закону збереження енергії лежить однорідність часу, тобто рівнозначність всіх моментів часу, що полягає в тім, що заміна моменту часу t₁ моментом часу t₂ без зміни значень координат і швидкостей тіл не змінює механічних властивостей системи. Поводження системи, починаючи з моменту t₂ , буде таким же, яким воно було б, починаючи з моменту t₁ .

Закон збереження енергії має загальний характер. Він застосовний до усім без винятку процесам, що відбуваються в природі. Повна кількість енергії в ізольованій системі тіл і полів завжди залишається постійним; енергія лише може переходити з однієї форми в іншу. Цей факт є проявом не знищення матерії і її рухи.

Причиною зміни швидкості тіла завжди є його взаємодія з іншими тілами. При взаємодії двох тіл завжди змінюються швидкості, тобто здобуваються прискорення. Відношення прискорень двох тіл однаково при будь-яких взаємодіях. Властивість тіла, від якого залежить його прискорення при взаємодії з іншими тілами, називається інертністю. Кількісною мірою інертності є маса тіла. Відношення мас взаємодіючих тіл дорівнює зворотному відношенню модулів прискорень. Другий закон Ньютона встановлює зв'язок між кінематичною характеристикою руху – прискоренням, і динамічними характеристиками взаємодії – силами. 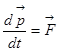, або, у більше точному виді, , тобто швидкість зміни імпульсу матеріальної крапки дорівнює діючої на нього силі. При одночасній дії на одне тіло декількох сил тіло рухається із прискоренням, що є векторною сумою прискорень, які виникли б при впливі кожної із цих сил окремо. Діючі на тіло сили, прикладені до однієї крапки, складаються за правилом додавання векторів. Це положення називають принципом незалежності дії сил. Центром мас називається така крапка твердого тіла або системи твердих тіл, що рухається так само, як і матеріальна крапка масою, рівній сумі мас всієї системи в цілому, на якій діють та ж результуюча сила, що й на тіло. . Проінтегрував це вираження можна одержати вираження для координат центра мас. Центр ваги - крапка додатка рівнодіючої всіх сил ваги, що діють на частки цього тіла при будь-якому положенні в просторі. Якщо лінійні розміри тіла малі в порівнянні з розміром Землі, то центр мас збігається із центром ваги. Сума моментів всіх сил елементарні ваги щодо будь-якої осі, що проходить через центр ваги, дорівнює нулю.

Потенційна енергія характеризує взаємодіючі тіла, кінетична – що рухаються. І та, і інша виникають у результаті взаємодії тел. Якщо кілька тіл взаємодію між собою тільки силами тяжіння й силами пружності, і ніякі зовнішні сили на них не діють (або ж їх рівнодіюча дорівнює нулю), те при будь-яких взаємодіях тіл робота сил пружності або сил тяжіння дорівнює зміні потенційної енергії, узятої із протилежним знаком. У той же час, по теоремі про кінетичну енергію (зміна кінетичної енергії тіла дорівнює роботі зовнішніх сил) робота тих же сил дорівнює зміні кінетичної енергії.

.

Із цієї рівності треба, що сума кінетичної й потенційної енергій тіл, що становлять замкнуту систему й взаємодіючих між собою силами тяжіння й пружності, залишається постійної. Сума кінетичної й потенційної енергій тіл називається повною механічною енергією. Повна механічна енергія замкнутої системи тіл, взаємодіючих між собою силами тяжіння й пружності, залишається незмінної. Робота сил тяжіння й пружності дорівнює, з одного боку, збільшенню кінетичної енергії, а з іншого боку - зменшенню потенційної, тобто робота дорівнює енергії, що перетворилася з одного виду в іншій.

2. Гідростатика. Рівновага рідин і газів

Гідростатика – найбільш простий розділ гідроаеромеханіки, що досліджує ситуації, коли рух відсутнє або швидкість мала. Гідростатика дозволяє зрозуміти деякі властивості такої важливої гідродинамічної величини, як тиск. Тиск на опору роблять і тверді, і сипучі речовини, але воно відрізняється від гідростатичного. Тиск твердого тіла визначається його вагою, тиск рідини – її глибиною. Сила тиску р на дно посудини не залежить від його форми, а визначається тільки рівнем налитої в посудину рідини відповідно до гідростатичної формули:

p = р_о + рgh

де р – щільність рідини, g – прискорення вільного падіння, h – глибина занурення, р_о – атмосферний тиск.

Сипучі тіла, подібно рідині й газу, можуть натискати на бічну поверхню, але для такого тиску не виконується закон Паскаля, що затверджує, що тиск у будь-якому місці спочиваючої рідини іл газу в усіх напрямках однаково, причому тиск однаково передається по всім обсязі рідини або газу. У законі Паскаля вага рідини або газу не враховується.

До основних законів гідростатики, крім закону Паскаля й гідростатичної формули, можна віднести закон Архімеда: на занурене в рідину або газ тіло діє сила, що виштовхує, рівна по величині ваги витиснутої рідини (або газу), спрямована проти сили тяжіння й прикладена до центра ваги витиснутого обсягу.

Якщо занурене в рідину тіло замінити такою ж рідиною, то вийде стан рівноваги - на поверхню тіла діє сила тиску рідини, що врівноважує вагу рідини усередині поверхні.

Рух рідин і газів.

Рух рідин і газів, як і всі інші види руху, розглянуті в механіці, можна повністю охарактеризувати, оперуючи одиницями виміру довжини, часу й сили. Так, діаметр парашута можна вимірювати в метрах, час зниження, скажемо, на 100 метрів – у секундах, а вага вантажу – у ньютонах. Точно так само вхідний перетин насоса можна вимірювати у квадратних метрах, об'ємна витрата середовища – у кубічних метрах у секунду, а потужність – у ньютон-метрах (джоулях) у секунду. Існує багато способів виміру таких характеристик плину з використанням різних – механічних і електричних – еквівалентів лінійки, годин і пружинних ваг. Наприклад, швидкість рідин і газів можна оцінювати по числу обертів в одиницю часу проградуїрованої крильчатки (гідрометрична вертушка й анемометр) або по зміні електроспротиву дроту, що нагрівається минаючим струмом, (дротовий термоанемометр); тиск можна визначати по викликуваному їм відхиленню вигнутої трубки або мембрани (манометр Бурдона й барометр-анероїд) або по струму, генеруємому пьезокристалом.

Прогнозування характеристик плину.

Якби такі виміри руху рідин і газів були єдиним заняттям гідроаеромеханіки, це була б дисципліна досить вузького профілю. Набагато більше важливе значення, чим вимір, має точне прогнозування характеристик плину при заздалегідь відомих або передбачуваних умовах. Очевидно, що недостатньо вміти просто виміряти пропускну здатність побудованого водозливу, - потрібно спочатку надійно спроектувати водозлив, розрахований на максимально можливий потік; точно так само виміряти лагом швидкість судна в плаванні простіше, ніж заздалегідь указати потужність двигунів, які будуть потрібні новому судну для підтримки заданої крейсерської швидкості; надрукувати в газеті швидкість вітру й атмосферний тиск, обмірювані вчора, набагато легше, ніж пророчити погодні умови на завтрашній день. Коротше кажучи, щирий предмет гідроаеромеханіки - установлення співвідношень між різними характеристиками плину, що дозволяють визначити кожну з них, як тільки задані інші характеристики, від яких вона залежить.

Рівняння нерозривності.

Хоча гідроаеродинаміка заснована на трьох добре відомих в механіці законах збереження маси, імпульсу й енергії, формулювання цих законів у ній виглядають складніше. Наприклад, звичайне визначення закону збереження маси говорить, що маса системи тіл залишається незмінної. Для рідини, що тече в трубі, цей закон використовується у формі, називаної рівнянням нерозривності. Рівняння нерозривності - співвідношення між швидкістю плину, об'ємною витратою середовища й відстанню між лініями струму. Це рівняння виражає один з основних законів гідроаеромеханіки, відповідно до якого об'ємна витрата у всякій трубці струму, обмеженої сусідніми лініями струму, повинен бути в будь-який момент часу однаковий у всіх її поперечних перерізах. Оскільки об'ємна витрата Q дорівнює добутку швидкості поточного середовища V на площу A поперечного перерізу трубки струму, рівняння нерозривності має такий вигляд:

Q = V₁ A₁ = V₂ A₂

або ж vS = const ( v – швидкість рідини, S – площа перетину труби, по якій тече рідина. Зміст - скільки води вливається - стільки й повинне вилитися, якщо умови плину незмінні).

Тому там, де перетин великий і лінії струму розріджені, швидкість повинна бути мала, і навпаки. (Всі три частини цієї подвійної рівності повинні виражатися в одній і тій же системі одиниць. Так, якщо величина Q виражена в м³ /з, те швидкість V повинна виражатися в м/с, а площа A – у м² .)

Рівняння Бернуллі.

Одне з найважливіших рівнянь гідромеханіки було отримано в 1738 році швейцарським ученим Данилом Бернуллі. Йому вперше вдалося описати рух нестисливої ідеальної рідини (сили тертя між елементами ідеальної рідини, а також між ідеальною рідиною й стінками посудини відсутні). Рівняння Бернуллі має вигляд:

р + рv² + pgh = const.

2