Курсовая работа: Вывод уравнения Лапласа. Плоские задачи теории фильтрации

В обоих случаях дебиты скважин, равноудаленные от середины или от концов батареи, будут одинаковы, а при разной удаленности будут отличаться. Последнее вызывается не одинаковой интенсивностью влияния со стороны скважин батареи на те или иные скважины. При этом при нечетном числе скважин дебит средней скважины отличается от дебитов других скважин.

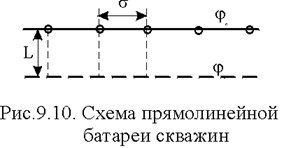
Дебиты равномерно расположенных скважин можно определить общим методом с использованием формулы (4.2). Можно вывести аналогичные уравнения для любой скважины прямолинейной батареи конечной длины в пласте с прямолинейным контуром питания, но с использованием дополнительно метода отображения. В этом случае запись уравнений оказывается громоздкой из-за необходимости учета не только взаимных расстояний между скважинами, но также расстояний между скважинами и воображаемыми источниками и расстояний между этими последними.

Для практических расчетов можно использовать приближенную формулу П.П. Голосова для общего дебита скважин прямолинейной батареи: для нечетного числа скважин 2n+1, где n - любое целое число

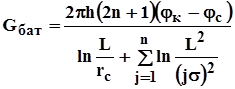
; (4.30)

для четного числа скважин 2n

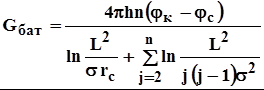
.(4.31)

Здесь h - толщина пласта; s - расстояние между скважинами; L – расстояние до контура.

Ошибка в определении дебитов по данным формулам не превышает 3-4% при L=10км, rс=10см при расстояниях между скважинами 100м£s£500м.

Приведенные формулы можно использовать при любом контуре питания, т.к. проведенные ранее исследования взаимодействия двух скважин показали, что форма контура питания пласта мало влияет на взаимодействие скважин. Что касается расстояния скважин до контура питания, то по мере приближения скважин к контуру питания эффект взаимодействия уменьшается, но в реальных условиях значительного удаления скважин от контура питания погрешность определения расстояния до контура даже в 100% не отражается значительно на эффекте взаимодействия. Для однородных пластов и жидкостей относительные изменения дебитов скважин, вызванные эффектом взаимодействия, не зависят от физико-геологических характеристик пласта и от физических параметров жидкости.

Рассмотрим теперь фильтрационное поле (рис. 4.10), поддерживаемое, для простоты, бесконечной цепочкой равностоящих скважин (требование бесконечности приводит к ликвидации граничных эффектов на концах батареи и равнодебитности скважин, т.к. все скважины оказываются в равных условиях притока к ним флюидов).

Для получения формул дебита скважины бесконечной прямолинейной батареи использует формулу (4.25) дебита скважины кольцевой батареи. Положим, что

rк=l+a;

a=ns /(2p ), (4.32)

где L=const - разность между радиусом контура питания и радиусом кольцевой батареи а; s=const - длина дуги окружности радиусом а между двумя соседними скважинами кольцевой батареи.

Подставив значения rк , a в формулу (4.25), получим

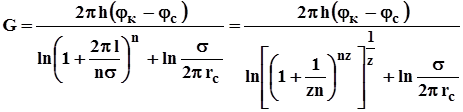,(4.33)

где

z=s / (2pl).

Переходя в данной формуле к пределу при n®¥ и учитывая, что

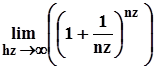=e,

получим формулу массового дебита скважины прямолинейной батареи

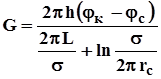. (4.34)

Здесь L - расстояние от контура питания до батареи;s - расстояние между скважинами батареи; h - толщина пласта.

Суммарный дебит из n - скважин определится следующим выражением

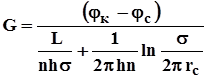.(4.35)

Для несжимаемой жидкости соотношение (4.35) можно переписать через давление и объёмный дебит

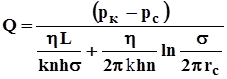. (4.36)

Ортогональная сетка, изображающая фильтрационное поле бесконечной прямолинейной батареи, изображено на рис. 4.11 .