Курсовая работа: Застосування координатного методу в стереометрії
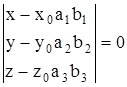(7)
Розкриваючи по елементах першого стовпчика визначник, отримаємо рівняння площини у вигляді:
Ax+By+Cz+D=0 (8)
де
.
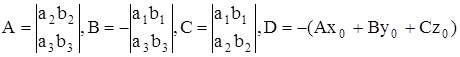Рівняння (8) є загальним рівнянням площини.
Приклад. Нехай задано М0 (8,-5,6) та 
та 
. Треба записати рівняння площини.
Розв’язання. Згідно (8) визначаємо параметри загального рівняння площини:
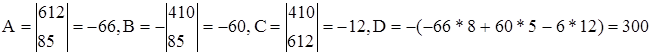
Таким чином, рівняння площини має вигляд:
-66x-60y-12z+300=0
3. Умова паралельності та перпендикулярності двох прямих, двох площин, прямої та площини у просторі.
Нехай є дві площини
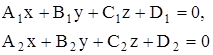(9)
З’ясуємо, за яких умов ці площини : а) паралельні; б) перепендикулярні.
Оскільки A1 ,B1 ,C1 –координати вектора 
, що перпендикулярний першій площині, а A2 ,B2 ,C2 –координати вектора 
, що перпендикулярний другій площині, то площини паралельні, якщо вектори , 
паралельні, тобто якщо їх координати пропорціональні:
.
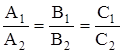Ця умова разом з тим достатня для паралельності площин ,якщо вони не співпадають.
Для того, щоб площини (9) були перпендикулярні, необхідно та достатньо, щоб вказані вектори 
, були перпендикулярні, що для ненульових векторів еквівалентно умові:
або А1 А2 + В1 В2 + С1 С2 =0.
Приклад. Нехай задано дві площини:
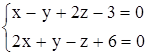
Треба з’ясувати їх взаємне розташування. В даному випадку маємо:
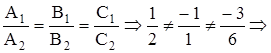площини не паралельні.
1*2-1*1-2*1=-1
площини не перпендикулярні.
Таким чином, площини розташовані під деяким углом, відмінним від ноля та дев’яноста градусів.
Нехай є площина та пряма, задані рівняннями:
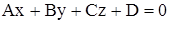
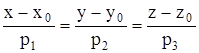
Оскільки вектор 
перпендикулярний площині, а вектор 
паралельний прямій, то пряма та площина паралельні, якщо ці вектори перпендикулярні, тобто якщо
(10)
Якщо при цьому точка ( x0 , y0 ,z0 ), що належить прямій, задовольняє рівнянню площини
то пряма розташована у площині.