Курсовая работа: Застосування координатного методу в стереометрії

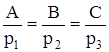(11)

Нехай дві прямі задані рівняннями в канонічній формі:

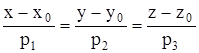(12)

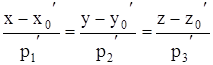(13)

Оскільки вектор паралельний першій прямій, а вектор паралельний другій прямій, то прямі паралельні якщо

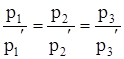
Зокрема, прямі співпадають, якщо при цьому точка першої прямої, наприклад (x₀ ,y₀ ,z₀ ) задовольняє рівнянню другої прямої, тобто якщо

.

Прямі перпендикулярні ,якщо вектори та перпендикулярні, тобто якщо

Приклад. Нехай задано площину та пряму:

Треба з’ясувати їх взаємне розташування.

Розв’язання. Маємо:

площина та пряма не паралельні;

площина та пряма не перпендикулярні.

Таким чином, площина та пряма розташовані у просторі під деяким кутом, відмінним від ноля та дев’яноста градусів.

4. Дведення координатним методом теореми про три перпендикуляри.

Теорема про три перпендикуляри : якщо пряма, проведена на площині через основу нахилої, перпендикулярна її проекції, то вона перпендикулярна нахилій. І навпаки: якщо пряма на площині перпендикулярна наклонній, то вона перпендикулярна і проекції нахилій.

Доведення . Нехай АВ- перпендикуляр до площини , АС –нахила та с- пряма в площині , що проходить через основу С нахилої (малюнок 3). Проведемо пряму , паралельну прямій АВ. Вона перпендикулярна площині . Проведемо через прямі АВ та площину . Пряма с перепендикулярна прямій . Якщо вона перпендикулярна прямій СВ, то вона перпендикулярна площині , тобто, і прямій АС.

Аналогічно, якщо пряма с перпендикулярна похилій СА то вона, будучи перпендикулярною і прямій , перпендикулярна площині , а значить, і проекції похилій ВС. Теорему доведено.

Того ж самого результату можна досягти, якщо скористатись координатним методом, попередньо задавши відповідні прямі їх напрямними векторами та послідовно використовуючи ознаки паралельності та перпендикулярності прямих у просторі.

Малюнок 2- Доведення теореми про три перпендикуляри.

5. Доведення методом координат ознаки паралельності двох площин.

Нехай завдані площини своїми рівняннями:

(14)

(15)

Оскільки координати загальної точки площин є розв’язанням системи рівнянь (14),(15) та кожне розв’язання системи рівнянь (14),(15) є координатами загальної точки площин , то питання про взаємне розташування двох площин зводиться до дослідження системи лінійних рівнянь (14),(15).

Позначимо через r та відповідно ранги матриць:

Якщо =2, r=1, то система рівнянь (14),(15) несумісна, тому площини не мають загальних точок, тобто паралельні.

6. Рівняння сфери. Властивість перетину кулі площиною.

Знайдемо рівняння сфери радіуса r з центром С (a, b, c) в прямокутній системі координат. Точка М простору належить цій сфері тоді та тільки тоді, коли СМ=r або СМ² =r² . Ця рівність в координатах запишеться таким чином:

(16 )

Це – рівняння сфери радіусу r з центром в точці С (a, b, c). Зокрема якщо центр сфери співпадає з початком координат, то a=b=c=0, тому рівність ( 16 ) набуває вигляду :

(17 )

Рівняння (16) можна записати у вигляді :