Курсовая работа: Зависящие от времени процессы в ядерном магнитном резонансе

Процессы спиновой релаксации за счет модуляции во времени различных взаимодействий – характерный, но далеко не единственный пример явлений, которые могут быть изучены методом ЯМР. Эти процессы в шкале времени ЯМР часто характеризуются либо очень малыми, либо очень большими временами. Понятие шкалы времени основано на простой концепции, которая находит применение во многих областях. Если речь идет о медленном процессе, то предполагается, что он может быть описан последовательно, на каждом из этапов. При рассмотрении быстрого процесса предполагается, что наблюдаем за неким усредненным поведением системы. Здесь необходимо сразу же пояснить, что понятие медленных и быстрых процессов вводится лишь тогда, когда приводится шкала времени, в которой проводится рассмотрение.

Простейший путь состоит в том, чтобы задать предельные значения времен, и в этом случае все физические явления описывать как быстрые или медленные по сравнению с этими значениями. Очевидно, что времена, задающие масштаб, зависят также и от того, какие физические процессы описываются в данном приближении. При этом существует не одна временная шкала ЯМР, а множество различных шкал в зависимости от типа рассматриваемых взаимодействий. С теоретической точки зрения наиболее сложной для обсуждения является промежуточная область, в которой не реализуются при предельных случаях: быстрых и медленных процессов. Независимо от используемой шкалы ЯМР физические процессы, связанные с различными движениями, обладают своей собственной шкалой времени, которая может быть описана временами корреляции или характеристическими частотами. В табл. представлены типичные интервалы частот для основных молекулярных движений: от очень медленных – с характеристическими временами от нескольких минут до нескольких часов до очень быстрых – в пикосекундной области.

Существуют разнообразные резонансные методы, позволяющие регистрировать процессы, протекающие с характерными временами до 10 нc. Только такие сверхбыстрые процессы, как торсионные и вибрационные движения атомов, не поддаются прямому наблюдению с помощью методов ЯМР. Кроме того существуют макроскопические движения: потоки жидкостей и мышечные сокращения. Эти процессы играют второстепенную роль в спектроскопии in-vitro, ориентированной на биохимические проблемы, однако в ЯМР-томографии и в in-vivo-спектроскопии роль таких процессов достаточно велика. Таким образом, характерные времена процессов, регистрируемых с помощью ЯМР, попадают в широкую область, охватывающую несколько порядков на временной шкале, при этом каждый из ЯМР-экспериментов характеризуется определенной временной областью, которая соответствует исследуемым процессам.

1. Временная корреляция и спектральная плотность

Молекулярные движения в жидкостях, например, вращения боковых цепей, не описываются определенными частотами на больших временных интервалах: мгновенная скорость вращения может варьироваться от одной боковой цепи к другой и от молекулы к молекуле, а за счет соударений с молекулами растворителя скорость вращения может изменяться как по величине, так и по направлению. Это означает, что молекулярные движения обладают широким спектром частот, который также присущ флуктуирующим магнитным полям, возникающим в результате движения атомов и молекул и ответственным за релаксационные процессы в спиновой системе.

Так как в растворе большое число одинаковых молекул находится в состояниях, характеризуемых разнообразными движениями, то при вычислении тех или иных величин проводят усреднение по ансамблю молекул, а также по большому промежутку времени. Поведение во времени какой-либо случайной величины f(Я),например, флуктуирующего магнитного поля, обычно описывают с помощью корреляционной функции

где угловые скобки означают усреднение по ансамблю, а черта – усреднение по времени. Усреднение по всем значениям времени tприменимо при описании стационарного состояния, для которого с точки зрения статистики не имеет значения, относительно какого момента времени определена корреляционная функция. Для случайных процессов таких, например, как движение молекул в состоянии термодинамического равновесия, корреляционная функция максимальна дляф= 0 и убывает во времени. Для большихфона должна стремиться к нулю, так как по определению для случайных процессов корреляции должны уменьшаться при условии, что наблюдение за системой ведется в течение достаточно длительного времени. Ширина корреляционной функции обычно описывается параметром, называемым временем корреляции T_c . Эта величина характеризует определенный вид движения и является мерой того, на каком временном интервале значения случайной величины еще можно рассматривать как коррелированные отлична от нуля.

Фурье - образ корреляционной функций Gi ф) называют спектральной плотностью J:

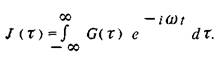
Точное значение времени корреляции и само определение этого параметра зависит от соответствующей корреляционной функции G, вид которой определяется конкретным физическим процессом. Во многих случаях корреляционную функцию можно достаточно хорошо описать экспонентой

Соответствующая спектральная плотность J, которую можно получить фурье - преобразованием этой корреляционной функции, имеет лоренцеву форму:

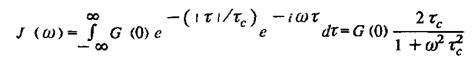
Для случая диффузии время корреляции обычно легко поддается интерпретации. Это среднее время между двумя соударениями данной молекулы с другими молекулами. Полуширина лоренцевой функции, как видно из, равна 1 /Tc. Таким образом, уменьшение времени корреляции, очевидно, расширяет спектральную область, на которой спектральная плотность отлична от нуля. Площадь под лоренцевой кривой постоянна и не зависит от времени корреляции.

Время корреляции T_c служит характерным параметром для проведения сравнений в шкале времени ЯМР, о которой речь шла ранее. Сама шкала времени определяется максимальной величиной взаимодействия Д. Процесс, характеризуемый временем корреляции T_c , является медленным, если

и соответственно быстрым, если Ао) Т_с

2. Химический обмен

Химический обмен – один из наиболее наглядных примеров динамических процессов. Сущность этого явления ясна из интуитивных соображений. Под химическим обменом в общем случае понимают процессы, в которых спин ядра в процессе релаксации может находиться в состояниях, характеризуемых различным химическим окружением, что соответствует различным параметрам ЯМР. В основе изменения окружения ядерного спина может лежать внутримолекулярный процесс, такой, например, как изменение конформации, или же межмолекулярный процесс. Здесь можно рассматривать исследуемое ядро в новой ковалентной структуре или же, наоборот, включать в рассмотрение межмолекулярные взаимодействия тех молекул, которые содержат данное ядро, и таким образом учитывать изменение окружения данного ядра. В простейшем случае имеется только два различных состояния, которые отличаются по химическому сдвигу д. Время корреляции T_c здесь представлено временами жизни T_a и T_b в состояниях AwBсоотвественно, а величина ДО) непосредственно определяется разностью химических сдвигов Д д =д_В – д_А , измеренной в единицах частоты. В этом случае медленный обмен определяется неравенством

а быстрый обмен -

где

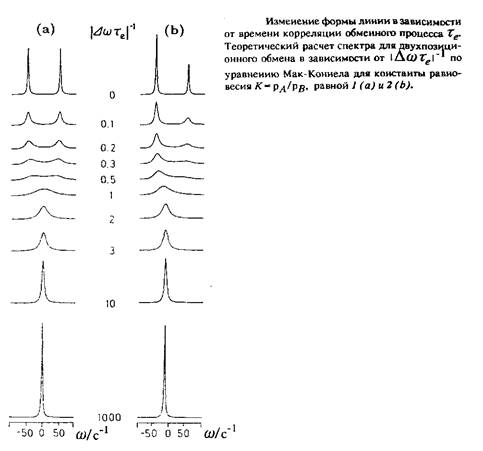
Соответствующие спектры ЯМР могут быть достаточно хорошо описаны обобщенными уравнениями Блоха, полученными в работе Мак-Коннела. Оба предельных случая: быстрого и медленного обмена, можно объяснить без привлечения серьезных расчетов, а чисто из интуитивных соображений путем предельных переходов X_e ~*0 и соответственно Xe ~* °°. В первом случае можно наблюдать лишь одну линию, так как ядро участвует в бесконечно быстром обмене между двумя состояниями с различным химическим окружением. Во втором случае можно наблюдать две резонансные линии с химическими сдвигами Oaи Ob, интенсивности которых прямо пропорциональны относительным заселенностям рли рв, т.е. в данном случае обмен вообще отсутствует. Усреднение положений резонансных линий при быстром обмене приводит к химическому сдвигу

Для описания поведения в промежуточной области такое простое соотношение отсутствует, однако можно вычислить в явном виде положение сигнала ЯМР как функцию времени корреляции обменного процесса T_e . Условия медленного обмена приводят к уширению обеих линий, а при ускорении обмена – к слиянию их в одну уширенную линию при выполнении условия IAox_e \ ~ 1. При дальнейшем возрастании скорости обмена линия будет сужаться до тех пор, пока ее ширина не станет равной ширине линии в отсутствие обмена.

Аналогичный процесс усреднения происходит и в случае других взаимодействий. Если окружения, соответствующие двум состояниям Л и В, различаются только константами косвенного спин-спинового взаимодействия J_a и J_b , то наблюдается мультиплет с усредненной константой J' =p_A J_A +p_B J_B js, oTexпор, пока для величины Al = J_А – J^г _в выполняется неравенство

Так как константы взаимодействия J, как правило, не коррелируют с разностью химических сдвигов, то в ряде случаев на основе этих констант должна быть установлена шкала времени, отличная от шкалы химических сдвигов. При наличии в спиновой системе взаимодействия, например косвенного спин-спинового, химический обмен не поддается описанию с помощью простых уравнений Мак-Коннела. Однако принципиально возможно описание поведения такой системы с привлечением квантово-механических подходов.

Какую биохимическую информацию можно извлечь из изучения процессов, связанных с химическим обменом? В области быстрого обмена в принципе можно рассчитать населенности отдельных состояний при условии наличия некоторой дополнительной информации. При этом наиболее важной является информация о числе состояний, участвующих в быстром обмене, так как это число присутствует в расчетной формуле в качестве параметра.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--