Курсовая работа: Зависимость потребления бензина от количества автомобилей
2) Подтвердилась ли гипотеза о том, что зависимость между ![]() и
и ![]()
близка к квадратичной?
3) Какая из двух кривых - прямая или парабола - меньше отклоняется от точек выборки (![]() ) ?
) ?
Диаграмма рассеивания
Даны выборки ![]() и
и ![]() , которые можно интерпретировать следующим образом:
, которые можно интерпретировать следующим образом: ![]() — потребление бензина,
— потребление бензина, ![]() — количество автомобилей. Задача состоит в изучении характера зависимости между
— количество автомобилей. Задача состоит в изучении характера зависимости между ![]() и
и ![]() . Исходные выборки представлены в таблице:
. Исходные выборки представлены в таблице:
| X | Y | X | Y | X | Y | X | Y |
| 8,64558 | 116,76 | 22,2483 | 112,8 | 35,3723 | 113,328 | 48,6586 | 125,396 |
| 9,30954 | 115,72 | 22,38 | 114,03 | 35,8685 | 119,397 | 49,2468 | 126,783 |
| 9,54538 | 109,996 | 22,743 | 114,952 | 36,0494 | 124,624 | 49,0515 | 125,652 |
| 9,91695 | 126,634 | 23,0127 | 117,027 | 36,5302 | 118,734 | 49,7645 | 119,88 |
| 10,3459 | 112,28 | 23,9216 | 110,664 | 36,7256 | 126,531 | 50,6983 | 129,604 |
| 11,1794 | 115,564 | 24,7213 | 120,474 | 37,2568 | 125,601 | 50,4538 | 125,877 |
| 12,0403 | 116,048 | 25,2151 | 120,749 | 38,6184 | 121,974 | 51,7368 | 124,935 |
| 12,4383 | 114,524 | 25,5633 | 125,365 | 38,669 | 123,196 | 52,3859 | 121,572 |
| 12,8887 | 114,716 | 26,5224 | 117,494 | 39,2617 | 119,925 | 52,932 | 127,416 |
| 13,3673 | 107,328 | 26,654 | 112,982 | 40,1783 | 122,293 | 53,1557 | 123,507 |
| 13,5643 | 114,422 | 26,7975 | 112,34 | 40,239 | 120,465 | 54,0261 | 128,29 |
| 14,4435 | 118,925 | 27,6272 | 127,172 | 41,1804 | 122,419 | 54,4972 | 136,727 |
| 14,4909 | 123,297 | 28,2653 | 121,229 | 40,8874 | 127,014 | 54,3892 | 125,732 |
| 15,3408 | 119,606 | 28,6799 | 119,246 | 42,0704 | 133,402 | 55,475 | 124,107 |
| 15,5866 | 116,443 | 28,9424 | 113,728 | 42,7372 | 136,142 | 55,7691 | 128,79 |
| 16,9966 | 119,384 | 29,8652 | 124,189 | 42,8423 | 123,36 | 55,912 | 139,417 |
| 17,4323 | 116,428 | 30,2303 | 131,775 | 43,6994 | 128,363 | 56,6281 | 127,151 |
| 17,2341 | 123,058 | 30,6092 | 113,164 | 44,4041 | 118,225 | 57,6097 | 130,697 |
| 17,7988 | 116,349 | 31,6162 | 122,517 | 45,0372 | 126,604 | 57,3441 | 142,839 |
| 18,5831 | 116,665 | 32,1788 | 117,256 | 45,1258 | 127,831 | 58,699 | 134,079 |
| 19,4722 | 118,844 | 32,7243 | 114,794 | 45,4427 | 122,39 | 59,0407 | 130,316 |
| 19,8208 | 123,205 | 32,7933 | 130,624 | 46,3461 | 129,182 | 59,3109 | 129,148 |
| 20,6594 | 109,789 | 33,1236 | 133,529 | 46,5863 | 127,344 | 59,8175 | 135,398 |
| 20,8651 | 118,634 | 34,0453 | 123,582 | 47,3429 | 124,694 | 60,3217 | 131,061 |
| 21,0348 | 110,347 | 34,9061 | 135,169 | 47,7225 | 117,103 | 61,2562 | 126,388 |
Изобразим эти точки в виде точечного графика с соответствующими координатами (![]() ,
, ![]() ); для этого надо найти размах выборки по X и Y и выбрать соответствующий масштаб. Сначала находим
); для этого надо найти размах выборки по X и Y и выбрать соответствующий масштаб. Сначала находим ![]() и
и ![]() , затем размах выборки по X , которая вычисляется по формуле
, затем размах выборки по X , которая вычисляется по формуле ![]() и в результате равна 52,61062. Аналогично
и в результате равна 52,61062. Аналогично ![]() и
и ![]() , а размах выборки поY получим равный 35,511. Глядя на размах выборок по X и по Y , выбираем масштаб диаграммы рассеивания и строим её.
, а размах выборки поY получим равный 35,511. Глядя на размах выборок по X и по Y , выбираем масштаб диаграммы рассеивания и строим её.

рис.1. Диаграмма рассеивания
По формуле  где
где 
можно найти коэффициент корреляции:
![]()
Он не равен нулю, следовательно, зависимость между X и Y существует.
Построение прямой y=ax+b, наименее отклоняющейся от точек (Xi ;Yi )в среднем квадратичном
Для построения прямой y = ax + b , наименее отклоняющейся от точек ![]() в среднем квадратичном, необходимо методом наименьших квадратов определить числа a, b такие, что функция двух переменных
в среднем квадратичном, необходимо методом наименьших квадратов определить числа a, b такие, что функция двух переменных ![]() принимает минимальное значение. Данная функция имеет вид:
принимает минимальное значение. Данная функция имеет вид:
![]() .
.
Зная, что необходимым условием минимума функции является равенство нулю ее первых частных производных, имеем следующую систему для нахождения значений ![]() :
:
 ,
, 
Данная система может быть представлена в виде:
 ,
,
где 
В результате получим что:

Докажем теперь, что в точке ![]() функция
функция ![]() имеет минимум. Достаточным условием существования экстремума функции двух переменных является следующее неравенство:
имеет минимум. Достаточным условием существования экстремума функции двух переменных является следующее неравенство:
![]()
![]() .
.
Для доказательства введем следующие обозначения:

Составим дискриминант ![]() . Тогда, если
. Тогда, если ![]() , то функция имеет в точке экстремум, а именно минимум при А>0 (или С>0). Из системы видно, что эти условия выполняются:
, то функция имеет в точке экстремум, а именно минимум при А>0 (или С>0). Из системы видно, что эти условия выполняются: ![]() =
= ![]() , С=200>0.
, С=200>0.
То есть точка ![]() действительно является точкой минимума.
действительно является точкой минимума.
Следовательно, функция ![]() при данных значениях
при данных значениях ![]() имеет следующий график:
имеет следующий график:
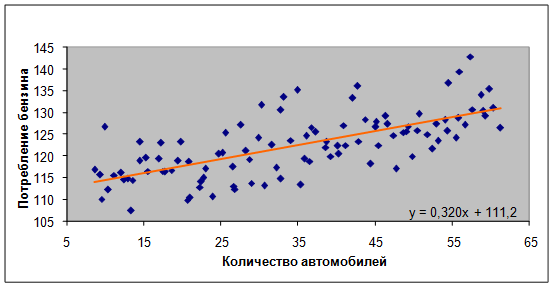
рис.2. График уравнения линейной регрессии