Курсовая работа: Зависимость высоты дерева от среднегодовой температуры
В нашем случае ![]() = 30,1964 ,
= 30,1964 , ![]() = 269,5502.
= 269,5502.
Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии:
![]() .
.
![]() =5,495125,
=5,495125, ![]() =16,41798.
=16,41798.
Исправленная дисперсия : ![]()
S(x) = 30,50141, S(y) = 272,2729.
Выборочное исправленное среднее квадратическое отклонение: ![]()
![]() = 5,522808,
= 5,522808, ![]() = 16,50069.
= 16,50069.
Часто статистические данные дополняются графиками. Графики являются самой эффективной формой представления данных с точки зрения их восприятия. Статистические графики представляют собой условные изображения числовых величин и их соотношений посредством линий, геометрических фигур, рисунков или географических карт-схем. Таким образом, облегчается рассмотрение статистических данных, они становятся наглядными, выразительными, обозримыми.
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны частоте ![]() .
.
Гистограммой относительных частот называется диаграмма, на которой изображены столбцы, при этом ось Х — это интервалы, а ось У — это относительная частота встречаемости:
![]() .
.
Полигоном частот называют ломаную, отрезки которой соединяют точки ![]() . Для построения полигона на оси абсцисс откладывают варианты
. Для построения полигона на оси абсцисс откладывают варианты ![]() , а на оси ординат соответствующие им частоты
, а на оси ординат соответствующие им частоты ![]() .
.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки ![]() . Для построения полигона на оси абсцисс откладывают варианты
. Для построения полигона на оси абсцисс откладывают варианты ![]() , а на оси ординат соответствующие им относительные частоты
, а на оси ординат соответствующие им относительные частоты ![]() .
.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию ![]() , определяющую для каждого значения
, определяющую для каждого значения ![]() относительную частоту события
относительную частоту события ![]() . По определению
. По определению ![]() , где
, где ![]() — число вариант, меньших
— число вариант, меньших ![]() ; n — объем выборки. Функция
; n — объем выборки. Функция ![]() обладает теми же свойствами, что и вероятность.
обладает теми же свойствами, что и вероятность.
Нормальное распределение — приближённая плотность вероятности.
Плотность нормального распределения имеет вид:
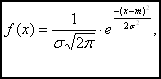
а функция распределения
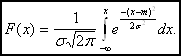 .
.
Исходные данные и их обработка
Дана выборка (объема n=100), зависимости числа Y от числа X.
| X | Y | X | Y |
| 15 | 49,4 | 8,98 | 30,5 |
| 0,212 | 5,46 | 10,6 | 34,5 |
| 17,9 | 57,2 | 16,8 | 53,3 |
| 7,68 | 26,9 | 2,7 | 11,6 |
| 18 | 56,5 | 7,58 | 25,9 |
| 14,9 | 48 | 12,3 | 40,4 |
| 13,4 | 43,3 | 4,06 | 16,5 |
| 0,358 | 4 | 0,244 | 5,02 |
| 0,994 | 7,23 | 4,86 | 17,7 |
| 9,78 | 31,2 | 9,48 | 31,4 |
| 5 | 18,3 | 15,7 | 50,9 |
| 6,68 | 24,1 | 13,5 | 41,8 |
| 17,7 | 57,3 | 16,6 | 52,7 |
| 1,99 | 8,87 | 12,1 | 38,6 |
| 19,7 | 61,4 | 15 | 49,6 |
| 7,16 | 23,9 | 12,2 | 41,2 |
| 10,8 | 37,1 | 8,06 | 28,1 |
| 0,652 | 6,42 | 17,6 | 56,4 |
| 9,72 | 32,4 | 19,7 | 62,7 |
| 12,6 | 40,1 | 9,98 | 34 |
| 4,78 | 15,9 | 16,4 | 50,9 |
| 1,36 | 7,43 | 17,8 | 54,7 |
| 4,94 | 17,2 | 5,42 | 17,4 |
| 12,3 | 38,8 | 6,98 | 22,4 |
| 4,64 | 17,4 | 5,98 | 19 |
Начнем изучение данных X и Y с построения диаграммы рассеивания:
Диаграмма рассеивания наглядно показывает тенденцию возрастания Y при возрастании Х. Это объясняется тем, что при увеличении количества рабочих дней, зарплата возрастает.
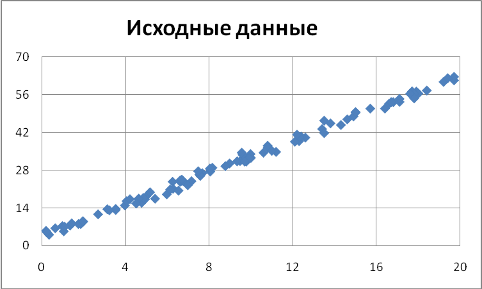
Теперь построим корреляционную таблицу. Разобьём значения x на 5 и y на 5 интервалов:
| y\x | 2 | 6 | 10 | 14 | 18 | N(y) | P*(y) |
| 7 | 18 | 0 | 0 | 0 | 0 | 18 | 0,18 |
| 21 | 1 | 27 | 1 | 0 | 0 | 29 | 0,29 |
| 35 | 0 | 0 | 20 | 7 | 0 | 27 | 0,27 |
| 49 | 0 | 0 | 0 | 9 | 7 | 16 | 0,16 |
| 63 | 0 | 0 | 0 | 0 | 10 | 10 | 0,1 |
| N(x) | 19 | 27 | 21 | 16 | 17 | 100 | |
| P*(x) | 0,19 | 0,27 | 0,21 | 0,16 | 0,17 | 1 |
По корреляционной таблице найдём оценки для Х:
выборочное среднее —![]() , где
, где ![]() :
:
![]() =9,4;
=9,4;
выборочную дисперсию — ![]() :
: