Лабораторная работа: Абсолютна та відносна похибка

3. Похибки добутку. Нехай

Аі=хі+∆хі (і = 1,2,...,n),

де для простоти вважатимемо, що хі > 0 (і -1, 2,..., п ), А = А1 А2 … Аn , u = х1х2… хn . Тоді

А = (х1 + ∆ х1 ) (х2 + ∆ х2) ... (хп + ∆хп) =

= х1х2 … хn + х2х3 … хn ∆ х1 + х1 х3… хn ∆ х2 + ... +

+ х1х2 … хn-1 + ∆хп + ... + ∆x1∆x2…∆xn .

Враховуючи зауваження, можемо прийняти, що

А = u +x1 x2 … хп + ∆х1+ х1 х3 … хп + ∆х2 +…+ x1 x2 … хn-1 + ∆хп .

Звідси

| ∆u | = | А – u | ≤ x2x3 … xn | ∆x1| + х1 х3… xn| ∆x2| +…+ + x1 x2 … хn-1 + ∆хп . (2)

Зокрема, якщо п = 2 , то

| ∆u | ≤ x2| ∆x1| + x1| ∆x2| .

За граничну абсолютну похибку добутку можна взяти

∆u = x2x3 … xn ∆x1+ х1 х3… xn ∆x2 +…+ x1 x2 … хn-1 + ∆хп .

Розділивши нерівність (5.1) на u, одержимо

Тоді за граничну відносну похибку добутку можемо прийняти

.

4. Похибки частки. Нехай A1 = х1 + ∆ х1, A2 = х2 + ∆ х2 , де для простоти будемо вважати, що x1 > 0, x2 > 0,, .

Тоді

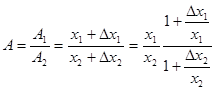i

.

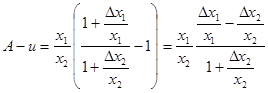Звідси

,

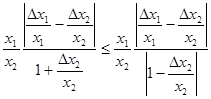aбo

.

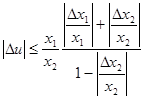Розділивши нерівність на u, одержимо

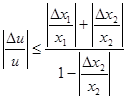
Врахувавши зауваження, замінимо на відносну похибку 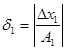діленого, - на відносну похибку 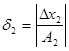дільника, - на відносну похибку частки. Отримаємо