Лабораторная работа: Идентификация и моделирование технологических объектов

Рисунок 5 – Схема модели компенсации люфта в среде Matlab

Полученные эпюры сигналов на входе (выходе) звена типа «люфт» и после компенсации изображены на рисунке 6.

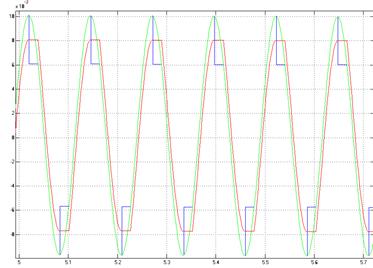
Рисунок 6 – Графики сигналов на входе звена типа «люфт» и после компенсации в среде Matlab

Выводы: в ходелабораторной работы я приобрел навыки моделирования нелинейного объекта типа «люфт», проанализировала их влияние на точность системы, составила и исследовала модель для компенсации люфта.

Оптимизация параметров пид-регуляторов для объектов управления с нелинейностями

Цель работы: освоение пакета прикладных программ NonlinearControlDesign (NCD) Blockset системы MATLAB для автоматической настройки параметров моделируемых систем электроприводов в условиях ограничений.

Индивидуальное задание:

Коэффициенты передаточной функции:

, , , .

Неопределенный параметр в диапазоне 0,2…0,5.

Желаемые параметры качества переходного процесса δ=±5%; σ=1,2; t_пп =1,5 с

Ход работы

Передаточная функция объекта (электропривода):

Коэффициент интегральной составляющей:

.

Коэффициент дифференциальной составляющих:

.

Пропорциональная составляющая (предельное значение):

.

Строим исследуемую схему в среде MatLab.

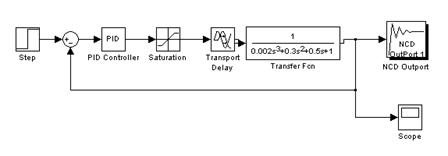
Рисунок 1 – Структурная схема модели для оптимизации ПИД-регулятора

Графики переходного процесса с оптимизированными параметрами ПИД-регулятора, представлены на рисунках 3-4.

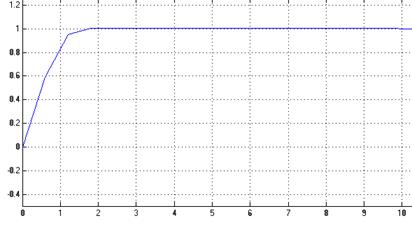
Рисунок 3 – График переходного процесса для заданной модели (Scope)

Параметры системы при оптимизации:

Starttime: 0 Stoptime: 60.

There are 2405 constraints to be met in each simulation.