Лабораторная работа: Иизучение прямолинейного движения тел на машине атвуда

a = 2b² (3.7)

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.

Измеренные значения и результаты их обработки приведены в таблице 4.1.

Результаты прямых и косвенных измерений Таблица 4.1

S 1 = 0,401 м		S 2 = 0,351 м		S 3 = 0,3 м		S 4 = 0,251 м		S 5 = 0,201 м
Номер измере­ния	=0,633 м1/2		= 0,592 м1/2		= 0,547 м1/2		= 0,5 м1/2		=0,448 м1/2
t , c	t 2 , c2	t , c	t 2 , c2	t , c	t 2 , c2	t , c	t 2 , c2	t , c	t 2 , c2
1	4,377	8,754	3,952	7,904	3,952	7,904	3,378	6,756	3,054	6,108
2	4,608	9,216	4,053	8,106	3,952	7,904	3,434	6,868	3,285	6,57
3	4,536	9,072	3,973	7,946	3,861	7,722	3,641	7,282	3,003	6,006
4	4,589	9,178	4,206	8,412	3,663	7,326	3,469	6,938	3,220	6,44
5	4,235	8,47	4,317	8,634	3,913	7,826	3,497	6,994	3,292	6,584
< t >, c	4,469		4,100		3,868		3,483		3,171
< t 2 >, c2	19,972		16,81		14,961		12,131		10,055

Средние значения времени <t > и квадрата времени < t ² > прохождения пути S, приведенные в таблице 4.1, рассчитаны по выражениям 3.1 и 3.2 (число точек измерения n=5 ).

Для определения случайной погрешности измерения, предварительно определим стандартную погрешность измерения, по формуле (3.4)

Для первой точки измерения (S ₁ = 40,1 см):

Δt₁ = t₁ −< t>₁ = 4,377-4,469= -0,092 с; Δt₁ ² = (-0,092)² = 0,008464с² ,

Δt₂ = t₂ −< t>₁ = 4,608 -4,469= 0,139 с; Δt₂ ² = (0,139)² = 0,019321с² ,

Δt₃ = t₃ −< t>₁ = 4,536-4,469= 0,067 с; Δt₃ ² = (0,067)² = 0,004489с² ,

Δt₄ = t₄ −< t>₁ = 4,589-4,469= 0,12 с; Δt₄ ² = (0,12)² = 0,0144 с² ,

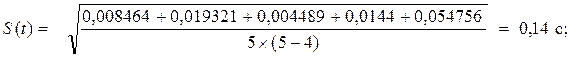Δt₅ = t₅ −< t>₁ = 4,235 -4,469= -0,234 с; Δt₅ ² = (-0,234)² = 0,054756 с² ,

Для второй точки измерения (S ₂ = 35,1 см):

Δt₁ = t₁ −< t>₁ = 3,952-4,100= -0,148 с; Δt₁ ² = (-0,148)² = 0,0219с² ,

Δt₂ = t₂ −< t>₁ = 4,053 -4,100= -0,047 с; Δt₁ ² = (-0,047)² = 0,00220с² ;

Δt₃ = t₃ −< t>₁ = 4,973-4,100= 0,873 с; Δt₁ ² = (0,873)² = 0,762с² ;

Δt₄ = t₄ −< t>₁ = 4,206-4,100= 0,094 с; Δt₁ ² = (0,094)² = 0,00883 с² ;

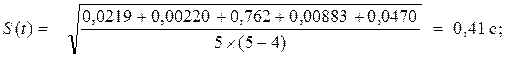Δt₅ = t₅ −< t>₁ = 4,317 -4,100= 0,217 с; Δt₁ ² = (0,217)² = 0,0470 с² ;

Для третьей точки измерения (S ₃ = 40,1 см):

Δt₁ = t₁ −< t>₁ = 3,952-3,868= 0,084 с; Δt₁ ² = (0,084)² = 0,00705с² ,

Δt₂ = t₂ −< t>₁ = 3,952 -3,868= 0,084 с; Δt₂ ² = (0,084)² = 0,00705с² ,

Δt₃ = t₃ −< t>₁ = 3,861-3,868= -0,007 с; Δt₃ ² = (-0,007)² = 0,000049с² ,

Δt₄ = t₄ −< t>₁ = 3,663-3,868= -0,205 с; Δt₄ ² = (-0,205)² = 0,0420 с² ,

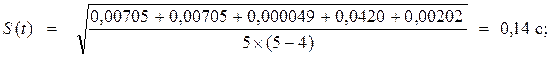Δt₅ = t₅ −< t>₁ = 3,913 -3,868= 0,045 с; Δt₅ ² = (0,045)² = 0,00202 с² ,

Для четвертой точки измерения (S ₄ = 25,1 см):

Δt₁ = t₁ −< t>₁ = 3,378-3,483= -0,105 с; Δt₁ ² = (-0,105)² = 0,0110с² ;

Δt₂ = t₂ −< t>₁ = 3,434 -3,483= -0,049 с; Δt₂ ² = (-0,049)² = 0,00240с² ;

Δt₃ = t₃ −< t>₁ = 3,641-3,483= 0,158 с; Δt₃ ² = (0,158)² = 0,0249с² ;

Δt₄ = t₄ −< t>₁ = 3,469-3,483= -0,014 с; Δt₄ ² = (-0,014)² = 0,00019 с² ;

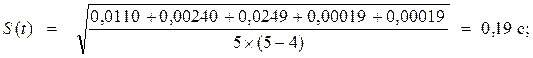Δt₅ = t₅ −< t>₁ = 3,497 -3,483= 0,014 с;