Лабораторная работа: Иизучение прямолинейного движения тел на машине атвуда

Для пятой точки измерения (S ₅ = 20,1 см):

Δt₁ = t₁ −< t>₁ = 3,054-3,171= -0,117 с; Δt₁ ² = (-0,117)² = 0,0137с² ,

Δt₂ = t₂ −< t>₁ = 3,285 -3,171= 0,141 с; Δt₂ ² = (0,141)² = 0,0199с² ,

Δt₃ = t₃ −< t>₁ = 3,003-3,171= -0,168 с; Δt₃ ² = (-0,168)² = 0,0282с² ,

Δt₄ = t₄ −< t>₁ = 3,220-3,171= 0,049 с; Δt₄ ² = (0,049)² = 0,00240 с² ,

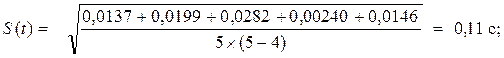Δt₅ = t₅ −< t>₁ = 3,292 -3,171= 0,121 с; Δt₅ ² = (0,121)² = 0,0146 с² ,

Таблица 4.2 Стандартная погрешность для каждой точки измерения

S1	S2	S3	S4	S5
S(t)	0,14	0,41	0,14	0,19	0,11
S ( t )	0,0196	0,1681	0,019	0,0361	0,121

Так, как доверительная вероятность α не оговорена в задании, то предположим, что доверительная вероятность α = 0,95. Тогда коэффициент Стьюдента t = 2,8.

Используя формулу (3.3) находим случайную погрешность для экспериментальных точек измерения.

Для первой точки измерения (S1).

Ơ (t)= 2,8*0,14=0,392.

Для второй точки измерения (S2).

Ơ (t)= 2,8*0,41=1,148.

Для третьей точки измерения (S3).

Ơ (t)= 2,8*0,14=0,392.

Для четвертой точки измерения (S4).

Ơ (t)= 2,8*0,19=0,532.

Для пятой точки измерения (S5).

Ơ (t)= 2,8*0,11=0,308.

Таблица 4.3

Случайная погрешность для каждой точки измерения

S1	S2	S3	S4	S5
Ơ (t)	0,392	1,148	0,392	0,532	0,308
Ơ ( t )	0,1536	1,3179	0,1536	0,283	0,0948

Так, как на миллисекундомере не обозначен класс точности прибора

и он является цифровым, то его погрешность составляет 1 единица

младшего разряда, т. е. 0.001 с. Тогда общая погрешность для каждой

из точек составит:

Для первой точки измерения (S1):

Δ(х)= 0,392+0,001=0,393.

Для второй точки измерения (S2):

Δ(х)= 1,148+0,001=1,149.