Математика / Лабораторная работа: Кривые разгона объекта управления

Лабораторная работа: Кривые разгона объекта управления

Перейдём к определению коэффициента а₂ . Для этого предварительно проинтегрируем исходное дифференциальное уравнение второго порядка (1), отбросив в нём на время уже определённое время чистого транспортного запаздывания. Получим:

(8)

Перепишем это уравнения для точки перегиба с координатами (t_п , x_вых (t_п )):

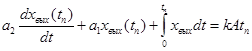. (9)

В уравнении (9):

(10)

а интеграл выражает площадь под кривой разгона до точки перегиба, поэтому обозначим его так:

. (11)

С учётом выражений (10) и (11) уравнение (9) примет вид:

(12)

Из этого уравнения и выведем формулу для определения последнего неизвестного коэффициента а₂ , получим:

. (13)

После определения всех коэффициентов дифференциального уравнения (1), перейдём к соответствующей ему передаточной функции, для чего уравнение (1) предварительно преобразуем по Лапласу, а затем найдём отношение изображения выходной величины объекта к входной (при нулевых начальных условиях), получим:

. (14)

Помня, что , а изображение входного ступенчатого сигнала имеет вид нетрудно получит изображение выходной величины:

. (15)

Далее, пользуясь известными из математики методами (например, разлагая правую часть выражения (15) на простые дроби при временном отбрасывании запаздывания, а затем учёте его в полученном выражении путём формальной замены ), получим уравнение расчётной кривой разгона апериодического объекта второго порядка с запаздыванием:

, при . (16)

По уравнению (16) и проводится проверка точности совпадения расчётной кривой разгона с экспериментальной, т.е. проверка адекватности математической модели объекта. В уравнении (16) p₁ и p₂ – корни характеристического уравнения объекта по рассматриваемому каналу, получаемого приравниванием знаменателя передаточной функции (14) к нулю, т.е. корни уравнения вида:

. (17)