Лабораторная работа: Математическое моделирование работы систем массового обслуживания

Если максимально допустимое число мест в очереди m конечно, то в СМО могут происходить отказы в предоставлении сервиса (система с отказами). Отклоняются от обслуживания те заявки, в момент прихода которых все места в очереди случайно оказались занятыми или при m = 0 (система без очереди) все каналы обслуживания оказались занятыми. В СМО с неограниченной длиной очереди (m = ¥) пришедшая заявка при невозможности немедленного обслуживания ожидает обслуживания при любой длине очереди и продолжительности времени ожидания.

По способу отбора из очереди заявок для обслуживания различают следующие виды дисциплины очереди:

1) первым пришел – первым обслуживается (FCFS);

2) последним пришел – первым обслуживается (LCFS);

3) случайный отбор заявок (SIRO);

4) ограничено время пребывания заявки в очереди;

5) с приоритетами, при которой некоторые находящиеся в очереди заявки имеют право первоочередного обслуживания (например, срочные работы выполняются раньше обычных).

По числу каналов обслуживания c различают одноканальные и многоканальные СМО. Многоканальные СМО разделяют:

· по характеристикам каналов – на однородные и неоднородные СМО;

· по расположению каналов – на СМО с параллельным и последовательным расположением сервисов.

В некоторых СМО интенсивность входного потока может зависеть от числа заявок, уже находящихся в системе (СМО замкнутого типа). В такой системе конечность очереди является следствием ограниченности мощности источника, создающего заявки на обслуживание. В СМО с источником бесконечной мощности (СМО разомкнутого типа) интенсивность входного потока практически не зависит от состояния системы.

3. Как определить основные функциональные характеристики СМО?

Наиболее употребляемыми функциональными характеристиками стационарных СМО являются следующие:

· p_отк – вероятность отказа в обслуживании (средняя доля заявок, получивших отказ в обслуживании):

– для СМО с отказами

;

– для СМО с неограниченной очередью

p_отк = 0;

· q – относительная пропускная способность системы (средняя доля обслуженных заявок; вероятность обслуживания)

q = 1 – p_отк ;

· – относительная нагрузка на систему

r = l / m;

· _эфф – эффективная интенсивность поступления заявок в систему (абсолютная пропускная способность системы; среднее число заявок, обслуживаемых системой в единицу времени)

· L_q – среднее число заявок в очереди (средняя длина очереди):

– для СМО без очереди

L_q = 0;

– для СМО с ограниченной очередью

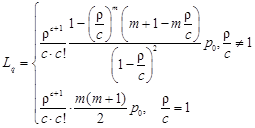
– для СМО с неограниченной очередью