Лабораторная работа: Математичні методи представлення знань

Приклад. Обчислити з точністю до 0,001 інтеграл

Р о з в ’ я з у в а н н я. За формулою (4) маємо:

при при

	-0,5	0,0000		-0,5	0,00000		0,05	0,0371
	-0,4	-0,1203		-0,45	-0,0946		0,10	0,0772
	-0,3	-0,1303		-0,40	-0,1203		0,15	0,1200
	-0,2	-0,1081		-0,35	-0,1304		0,20	0,1652
	-0,1	-0,630		-0,30	-0,1303		0,25	0,2122
	0	0,0000		-0,25	-0,1204		0,30	0,2607
	0,1	0,0772		-0,20	-0,1081		0,35	0,3103
	0,2	0,1652		-0,15	-0,0881		0,40	0,3610
	0,3	0,2607		-0,10	-0,0630		0,45	0,4121
	0,4	0,36098		-0,05	-0,0335		0,50	0,4637
	0,5	0,46365		0,00	0,0000

Отже,

.

Нехай деяка функціяf(x) задана в вузлах інтерполяції:

(i=1,2,3.,n) на відрізку [а,b] таблицею значень: .

Потрібно знайти значення інтегралу .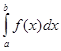

Спершу складемо інтерполяційний багаточлен Лагранжа:

Для рівновіддалених вузлів інтерполяційний багаточлен має вигляд:

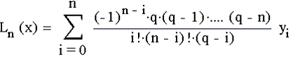
де q=(x-x0) /h – крок інтерполяції, замінимо підінтегральну функцію f(x) інтерполяційним багаточленом Лагранжа:

Поміняємо знак підсумовування і інтеграл і винесемо за знак інтеграла постійні елементи:

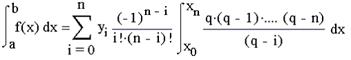
Оскільки dp=dx/h, то, замінивши межі інтеграції, маємо:

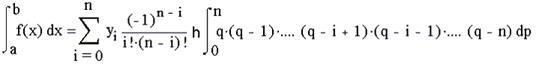
Для рівновіддалених вузлів інтерполяції на відрізку [а,b] величина крок визначається як h=(b-a)/n. Представивши цей вираз для h у формулу (4) і виносячи (b-a) за знак суми, отримаємо:

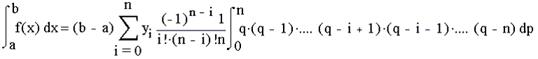
Покладемо, що

де i=0,1,2.,n; Числа називають коефіцієнтами Ньютона-Kотеса. Ці коефіцієнти не залежать від вигляду f(x), а є функцією тільки по n. Тому їх можна обчислити заздалегідь. Остаточна формула виглядає так:

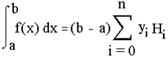
Формула трьох восьмих:

Якщо в формулі Ньютона-Котеса взяти n = 3, тобто функцію f(x) замінити інтерполяційним багаточленом третього степеня, побудованим за значення функції f(x) у точках x0=a, x1=a+h, x2=a+2h, x3=b, h=(b-a )/3. то одержимо таку квадратурну формулу:

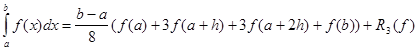де