Лабораторная работа: Определение момента инерции твердых тел 4

Работу выполнил студент группы 0ОП5а Кузнецов Д.А.

1. ЦЕЛЬ РАБОТЫ

Целью настоящей работы является определение момента инерции твердых тел и экспериментальная проверка справедливости теоремы Штей­нера на примере физического маятника.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

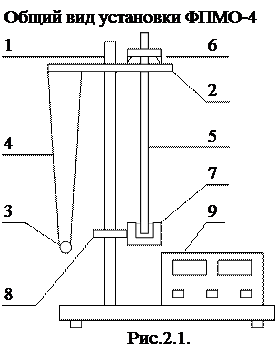??? ????????????????? ???????? ??????? ???????? ? ??????????? ??????? ??????? ? ?????? ?????? ???????????? ??????????? ????????? ?????????????? ???????? ???? - 4. ??? ?????????? ?????? (???. 4.1), ?? ???????????? ?????? ????????? 1 ???????? ???????? ????????? 2, ??????? ????? ??????????? ???????? ?????? ?????? ?? 360? ? ???????? ? ????? ????????? ?????????. ? ????? ??????? ?????????? 2 ???????? ?????????????? ???????, ? ? ?????? - ??????????. ?????????????? ??????? ???????????? ????? ????????????? ????? 3 ?? ?????????? ??????? 4. ?????????? ??????? - ???????? ???????? 5, ??????????? ?? ??????? ?????? 6. ??????? ?????? 6 ????? ???????????? ?? ???? ????? ??????? ? ????????????? ? ????????? ?????????.

Стержень 5 имеет кольцевые проточки, которые служат для надежной фиксации опорных призм. Установка снабжена фотоэлектрическим датчиком 7, который закреплен на вертикальной стойке с помощью кронштейна 8 и имеет возможность перемещаться как вдоль, так и вокруг стойки и фиксироваться в любом положении. Датчик предназначен для выдачи сигналов на миллисекундомер 9. Миллисекундомер физический выполнен самостоятельным прибором с цифровой индикацией времени и количества полных периодов колебаний маятника.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Средняя величина периода колебаний маятника:

T = t / n , (3.1)

где t - продолжительность 10 - 15 колебаний;

n - число колебаний за время t .

Формула для экспериментального расчета момента инерции прямого тонкого стержня

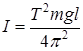, (3.2)

где T - период колебаний маятника;

l - расстояние от центра масс до точки подвеса маятника;

m - масса маятника;

g - ускорение свободного падения.

Формула для теоретического расчета момента инерции прямого тонкого стержня длиной d и массой m относительно оси, перпендикулярной к стержню и проходящей через его середину:

I₀ = md ² /12 (3.3)

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.

Результаты прямых и косвенных измерений представлены в таблице.

Таблица.

Данные измерений

Номер опыта	n	t , c	T , c	l2 , м2	I, кг×м2	Примечание
1	10	12,591	1,2591	0,03829	m = 358 г s(t ) = ± 2 мс d(m ) = 2%
2	10	12,280	1,2280	0,03107
3	10	12,095	1,2095
4	10	12,155	1,2155
5	10	12,781	1,2781
6	10	14,658	1,4658
7	10	21,096	2,1096

Подсчитаем среднюю величину периода колебаний маятника (3.1)

T₁ =12,591/ 10 = 1,2591

T₂ =12,280/ 10 = 1,2280
T₃ =12,095/ 10 = 1,2095
T₄ =12,155/ 10 = 1,2155
T₅ =12,781/ 10 = 1,2781
T₆ =14,658/ 10 = 1,4658
T₇ =21,096/ 10 = 2,1096

Теперь найдем момент инерции прямого тонкого стержня по формуле (3.2)

(1,25)² * 0,358 * 10 *0,27

I₁ = = 0,03829

--> ЧИТАТЬ ПОЛНОСТЬЮ <--