Лабораторная работа: Основи роботи в системі символьної математики MATLAB 5.2

-0.0862

Обчислення масиву косинусів тут пройшло коректно. А ось обчислення масиву функції sin(х)/х дає на перший погляд несподіваний ефект замість масиву з шістьма елементами обчислено єдине значення. Причина “парадоксу” тут в тому, що оператор / обчислює відношення двох матриць, векторів або масивів. Якщо вони однієї розмірності, то результат буде одним числом, що в цьому випадку і видала система. Щоб дійсно отримати масив значень sin(х)/х, треба використати спеціальний оператор почленного ділення масивів -./.

Тоді буде отримано масив чисел:

»sin(х)./х

Warning: Divide by zero.

ans =NaN 0.8415 0.4546 0.0470 -0.1892 -0.1918

Проте, і тут без особливостей не обійшлося. Так, при х=0 значення sin(х)/х дає невизначеність вигляду 0/0=1. Однак, як і всяка чисельна система, MATLAB класифікує спробу розподілу на 0 як помилку і виводить відповідне попередження. А замість очікуваного чисельного значення виводиться символьна константа NaN, що означає, що невизначеність 0/0 все ж не звичайне число. Формати чисел - команда format

При роботі з числовими даними можна задавати різні формати представлення чисел. Однак в будь-якому випадку всі обчислення проводяться з подвійною точністю. Для установки формату представлення чисел використовується команда »format name, де name – ім’я формату. Для числових даних name може бути наступним повідомленням: short - коротке представлення в фіксованому форматі (знаків), short е - коротке представлення в експонентному форматі (5 знаків мантиси і 3 порядки), long – довге представлення в фіксованому форматі (15 знаків), long е – довге представлення в експонентному форматі (15 знаків мантиси і 3 порядки), hex - представлення чисел в шістнадцятеричній формі; bank - представлення для грошових одиниць.

Основи роботи з векторами і матрицями.

Якщо необхідно задати вектор з трьох елементів, то їх значення треба перерахувати в квадратних дужках, розділяючи пропусками.

Задання матриці вимагає вказівки різних рядків. Для розрізнення рядків використовується знак - ; (крапка з комою). Цей же знак (або знак коми) в кінці введення запобігає виведенню матриці або вектора на екран дисплея. Так, введення.Можливе введення елементів матриць і векторів у вигляді арифметичних виразів, що містять будь-які доступні системі функції, наприклад:

»V=[2+2/(3+4) exp(5) sqrt(10)];

»V

V=

2.2857 148.4132 3.1623

Для вказівки на елемента вектора або матриці використовуються вирази вигляду V(i) або M(i;j). Якщо потрібно привласнити елементу M(i;j) нове значення х, потрібно використати вираз M(i;j)=х. Можливе завдання векторів і матриць з комплексними елементами.

Нарівні з операціями над окремими елементами матриць і векторів система дозволяє виробляти операції множення, розподілу і зведення в міру відразу над всіма елементами масивами. Для цього перед операцією ставиться знак точка. Наприклад, знак * означає знак множення для векторів або матриць, а знак .* - множення всіх елементів у вигляді масиву. Так, якщо М - матриця, то М.*2 дасть матрицю, всі елементи якої помножені на скаляр - число 2.

Об’єднання малих матриць у велику. Описаний спосіб завдання матриць дозволяє виконати операцію конкатенації – об’єднання малих матриць у велику. Для знаходження суми стовпчиків матриці використовується функція sum(A) , а суми рядків sum(A’) . Запис А’ означає транспонування матриці А. Видалення стовпців і рядків матриць. Для формування матриць і виконання ряду матричних операцій виникає необхідність видалення окремих стовпців і рядків матриці. Для цього використовуються пусті квадратні дужки

Для роботи з матрицями використовуються основні команди:

det (Х)- знаходження визначника матриці;

inv (X) – знаходження оберненої матриці.

3. Практична робота

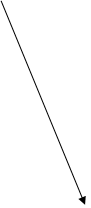
1.Задаємо матриці:

2. Визначаємо визначники і множення А·В і В·А:

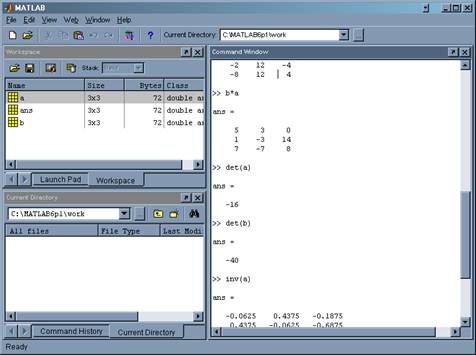
3.Знаходимо обернені матриці.

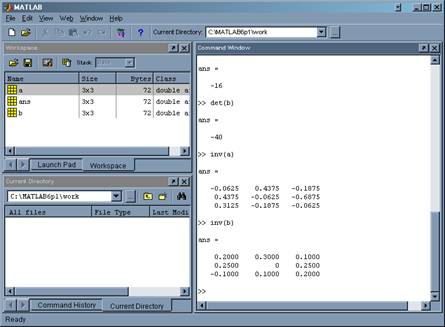
4. Задаємо матриці і знаходимо матрицю Х.