Лабораторная работа: Переоценка в основных фондах на предприятиях Перепись населения
N3 = 10000 / 2000 = 5 сберкасс
Найдем среднее число сберкасс в районе по формуле среднего арифметического:
= (6 + 6 + 5) / 3 = 5,667 сберкасс.
Средняя сумма вкладов на район города находиться по формуле средней арифметической:
= (5400 + 3900 + 8000) / 3 = 5766,667 млн. руб.
Средняя сумма вкладов на одну сберкассу находиться по формуле:
= (5400 + 3900 + 8000) / (6 + 6 + 5) = 1017,647 тыс. руб.
Практическая работа №5
В соответствии с макетом по данным табл. 2.1 постройте группировку предприятий по признакам: X –объем продукции,Y – производительность труда.
Вычислите общую, внутригрупповые и межгрупповую дисперсии производительности труда; среднюю из внутригрупповых. Проверьте сложением дисперсий правильность Ваших расчетов.
Вычислите коэффициент детерминации.
Сделайте краткие выводы.
Решение:
Рассчитаем производительность труда для каждого завода.
Таблица 5.1
| Заводы, п/п | Годовой объем продукции, млн. руб. | Производительность труда, тыс. руб. / чел. |
| 1 | 1,7 | 6,07 |
| 2 | 4,8 | 10,00 |
| 3 | 3,7 | 8,81 |
| 4 | 6,1 | 12,08 |
| 5 | 9,4 | 13,24 |
| 6 | 9,6 | 9,41 |
| 7 | 2,1 | 4,29 |
| 8 | 2,6 | 5,20 |
| 9 | 4,5 | 7,26 |
| 10 | 8,4 | 8,48 |
| 11 | 9,7 | 10,43 |
| 12 | 2,3 | 5,35 |
| 13 | 3,4 | 6,07 |
| 14 | 6,3 | 10,33 |
| 15 | 9,8 | 10,83 |
| 16 | 7,3 | 9,86 |
| 17 | 1,8 | 4,62 |
| 18 | 2,6 | 6,05 |
| 19 | 4,8 | 9,41 |
| 20 | 16,1 | 12,88 |
| 21 | 1,3 | 3,82 |
| 22 | 2,3 | 5,90 |
| 23 | 1,3 | 5,20 |
| 24 | 3,4 | 6,94 |
| 25 | 5,6 | 12,87 |
| 26 | 2,2 | 8,46 |
| 27 | 1,9 | 8,44 |
| 28 | 6,1 | 8,65 |
| 29 | 8,2 | 13,23 |
| 30 | 3,6 | 11,61 |
| 31 | 4,6 | 11,22 |
| 32 | 2,5 | 10,64 |
| Заводы, п/п | Годовой объем продукции, млн. руб. | Производительность труда, тыс. руб. / чел. |
| 33 | 3,4 | 8,61 |
| 34 | 6,4 | 16,20 |
| 35 | 2,3 | 6,57 |
| 36 | 1,8 | 9,00 |
| ИТОГО: | 173,9 | 318,0 |
Разделим выборку на 5 классов. Величины интервалов определим из формул:
, 
.
, 
.
Составим корреляционную таблицу
Таблица 5.2
| y | х | |||||||||||||
| 3,82 | 6,30 | 6,30 | 8,78 | 8,78 | 11,25 | 11,25 | 13,73 | 13,73 | 16,20 | Итого |  | |||
| 1,30 | 4,26 | 10 | 5 | 3 | 1 | 0 | 19 | 2,78 | ||||||
| 4,26 | 7,22 | 0 | 2 | 4 | 2 | 1 | 9 | 5,74 | ||||||
| 7,22 | 10,18 | 0 | 1 | 4 | 2 | 0 | 7 | 8,70 | ||||||
| 10,18 | 13,14 | 0 | 0 | 0 | 0 | 0 | 0 | 11,66 | ||||||
| 13,14 | 16,10 | 0 | 0 | 0 | 1 | 0 | 1 | 14,62 | ||||||
| Итого | 10 | 8 | 11 | 6 | 1 | 36 | - | |||||||
 | 5,06 | 7,54 | 10,01 | 12,49 | 14,96 | - | - | |||||||
Значения в строке и столбце задают последовательность точек, которая иллюстрирует зависимость среднего значения результативного признака (у) от факторного признака (х) – эмпирическую линию регрессии.
Общая и межгрупповая дисперсии находятся по формулам :
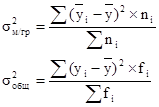
где 
- межгрупповая дисперсия; 
- общая дисперсия. 
- групповые средние; 
- общая средняя; ni - частота i-ой группы; yi – i-й вариант признака; fi – частота i-го варианта.
Общая дисперсия показывает вариацию результативного признака под воздействием всех факторов. Межгрупповая дисперсия показывает вариацию результативного признака, обусловленную вариацией группировочного. Средняя из внутригрупповых показывает вариацию результативного признака под воздействием факторов неучтенных при группировке. Средняя из внутригрупповых находиться по формуле средневзвешенной.
Все три вида дисперсий связаны правилом сложения трех дисперсий
= + 
Таблица 5.3 Вспомогательные расчеты для расчета межгрупповой дисперсии
| Группа | ni |  i | i – | (i – )2 | ni · (i – )2 |
| 1 | 19 | 6,93 | -1,91 | 3,63 | 69,00 |
| 2 | 9 | 10,89 | 2,06 | 4,23 | 38,09 |
| 3 | 7 | 10,78 | 1,95 | 3,80 | 26,60 |
| 4 | 0 | 0,00 | -8,83 | 78,05 | 0,00 |
| 5 | 1 | 12,88 | 4,05 | 16,37 | 16,37 |
| Итого | 36 | - | - | - | 150,06 |
= 150,06 / 36 = 4,168