Лабораторная работа: Планирование машинного эксперимента с имитационной моделью системы массового обслуживания

где i – номер фактора (i=1,n);

j – номер опыта (j=1,N ).

2. Условием нормировки, т.е. сумма квадратов элементов каждого столбца равна числу опытов:

_ij ² = N(i=1,n) (5 )

3.Ортогональностью, это означает, что сумма почленных произведений любых двух вектор- столбцов матрицы равна 0, т.е.

_{ij *} х_kj =0 (ik; i, k=1,n) (6 )

Данные свойства, особенно условие ортогональности, позволяют значительно упростить определение коэффициентов уравнения множественной регрессии. В этом случае оценки коэффициентов регрессионной модели можно вычислить по формуле:

a_i =_ij *y_j /N(i=0,n) (7 )

А коэффициенты парных взаимодействий соответственно по формуле:

a_ik =_ij *x_kj *y_j /N (ik; i, k=1,n) (8)

Количество испытаний в ПФЭ значительно превосходит число определяемых коэффициентов линейной модели плана эксперимента, т.е. ПФЭ обладает большой избыточностью и поэтому возникает проблема сокращения числа опытов. В связи с этим используется дробный факторный эксперимент (ДФЭ), который представляет часть полного факторного эксперимента. Матрица планирования для дробного факторного эксперимента называется дробной репликой. Различают регулярные и нерегулярные дробные реплики.

Регулярные реплики образуются из ПФЭ 2ⁿ делением пополам, на четыре части, восемь частей ит.д., т.е. на число кратное 2. Они называются соответственно: полурепликой, четверть- репликой, - реплики и т.д.. ДФЭ обозначается как 2^{n - k} , где

k – кратность деления ПФЭ 2ⁿ на части 2^k . Например, ДФЭ типа 4-2 означает, что ПФЭ из N=2⁴ =16 делится на 2² =4 и получается план эксперимента, состоящий из N=2^4-2 =4 опытов.

Если регулярные реплики умножить на нечетные числа, больше единицы, то получаются нерегулярные реплики. Как например, реплики, реплики, реплики и т.д. являются нерегулярными.

Использование ДФЭ позволяет значительно сократить количество экспериментов и тем самым сэкономить ресурсы ЭВМ.

2.2 Пример планирования машинного эксперимента для модели СМО

Пусть необходимо провести машинный эксперимент по определению функциональной зависимости среднего времени ожидания заявки в очереди (_ож ) от факторов: интенсивность поступления заявок λ, интенсивности обслуживания μ и емкости буфера L для однофазной одноканальной системы массового обслуживания со следующими параметрами: интенсивность поступления заявок λ=155; интенсивность обслуживания μ=105; количество мест в очереди L=102.

Для определения заданной зависимости представим математическую модель системы в виде:

y= a₀ +a₁ x₁ +a₂ x₂ +a₃ x₃ , (9)

x₁ = λ ; x₂ = μ; x₃ = L ; y=_ож

Так как порядок модели n=3, то матрица планирования для полного факторного эксперимента примет вид (Таблица 2).

Таблица 2. Матрица планирования для модели СМО

Номер опыта	х0	х1	х2	х3	y
1	+1	-1	-1	-1
2	+1	+1	-1	-1
3	+1	-1	+1	-1
4	+1	+1	+1	-1
5	+1	-1	-1	+1
6	+1	+1	-1	+1
7	+1	-1	+1	+1
8	+1	+1	+1	+1

При этом следует помнить, что кодированные значения факторов соответствуют -1 нижнему уровню фактора, а +1 верхнему уровню фактора:

· для интенсивности поступления заявок λ нижний уровень равен λ_k =10 , а верхний λ_b =20;

· для интенсивности обслуживания μ нижний уровень равен μ_k =5, а верхний 15 μ_b ;

· для количества мест в очереди L нижний уровень L_k =8и верхний L_b =12

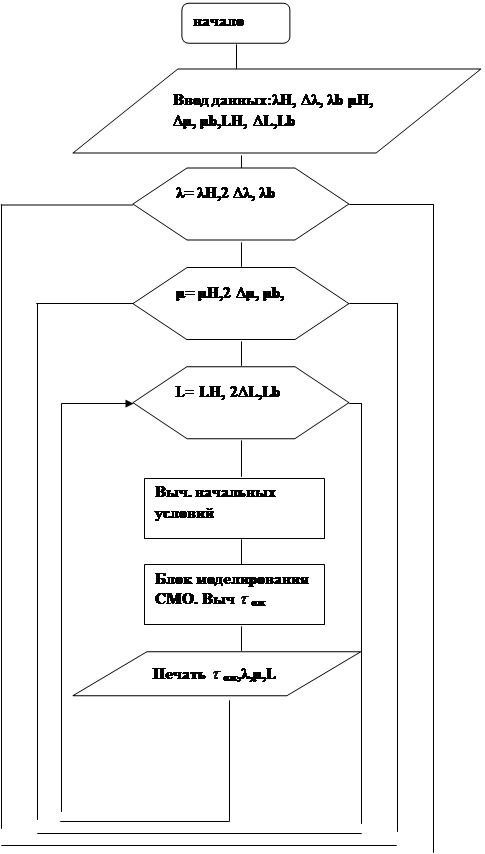
Поэтому при моделировании этих уровней факторов в блоке управления необходимо организовать их изменения. Это можно сделать путем введения нуля циклов. Тогда блок- схема управления вариантами моделирования примет вид (Рис1)

Рис1. Блок- схема управления вариантами моделирования

Для определения среднего времени ожидания _ож можно воспользоваться блок- схемой Рис лабораторной работы 3. Результаты моделирования заносятся в Таблицу 2 в колонку для y.