Лабораторная работа: Программирование в MATLAB
- S1''(x0)=0, S3''(x3)=0
- S1'(x0)=f '(x0), S3'(x3)=f '(x3)
- S1''(x0)=f «(x0), S3''(x0)=f «(x3)
· Для определения коэффициентов естественного кубического сплайна (краевые условия 1) необходимо решить следующую систему уравнений:
·
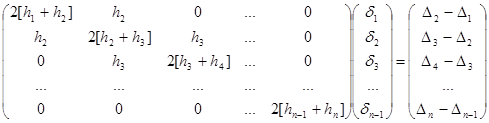
Коэффициенты σ0 =0,σn =0
· Построить графики исходной функции и сплайн-функций для всех трех типов краевых условий.
· Построить графики функций погрешности сплайн-интерполяции f(x) – S(x) для всех трех типов краевых условий.
· Рассчитать максимальные по модулю значения погрешности интерполяции на заданном промежутке [x0, xn] для каждого вида сплайна.
Примечание:
В пакете MATLAB индексы одномерных и двумерных массивов начинаются с 1, а не с 0. Учесть это при составлении программы.
Задание №3
Аппроксимация функции методом наименьших квадратов (МНК).
Данное задание подразумевает нахождение для некоторой совокупности данных аппроксимирующей функции (многочлена степени m), построенной методом наименьших квадратов (МНК).
Цель работы:
Необходимо составить программу нахождения коэффициентов многочлена φ( x )= a 0 + a 1 * x +… an * xm методом наименьших квадратов.
Рекомендации по выполнению работы:
Пусть, например, имеется следующая совокупность данных:
| х i | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 |
| yi | 8,3893 | 8,6251 | 8,9286 | 8,9703 | 9,1731 | 9,1784 | 8,8424 | 8,7145 | 8,3077 | 7,9611 |
Поиск необходимых коэффициентов осуществляется следующим образом:
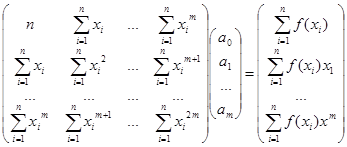
где n – количество точек (x , y ),
m – степень искомого многочлена,
a 0 , a 1 , …, am – искомые коэффициенты (φ ( x )= a 0 + a 1 x + … + am xm ).
Требования к программе
При выполнении данной работы необходимо:
· Задать границы отрезка [x1, xn], на котором строится аппроксимирующая функция φ(x)=a0+a1*x+… an * xm
· Задать m – степень многочлена
· Примечание: x1, xn, m вводятся с клавиатуры.