Лабораторная работа: Проведение выборочного наблюдения
Введение
Целью лабораторной работы является освоение методики организации и проведения выборочного наблюдения; статистических методов и методов компьютерной обработки полученной информации; методов оценки параметров генеральной совокупности на основе выборочных данных.
Выборочное наблюдение – важнейший вид не сплошного наблюдения. Теория выборочного наблюдения, т.н. выборочный метод, – совокупность принципов и способов отбора единиц совокупности, а также способов и методов оценки параметров генеральной совокупности на основе выборочных единиц. Выборочный метод в настоящее время получил широкое практическое применение, поскольку обладает целым рядом преимуществ по сравнению со сплошным наблюдением и иными видами несплошного наблюдения.
Преимущества выборочного наблюдения по сравнению со сплошным:
1. Экономия времени, финансовых, трудовых, материальных ресурсов.
2. Возможность расширить программу наблюдения.
С другими видами не сплошного наблюдения:
3. Благодаря хорошо разработанной теории выборки и используемых при выборочных наблюдениях способах формирования выборки появляется возможность дать вероятностную оценку параметров генеральной совокупности.
Генеральная совокупность – совокупность, которая собственно интересует исследователя и из которой отбираются единицы в выборочную совокупность. Выборочная совокупность – совокупность отобранных единиц, по которым будут фиксироваться значения тех или иных признаков.
Основной принцип формирования выборочной совокупности – случайность отбора, т.е. всем единицам генеральной совокупности должна быть обеспечена равная вероятность попадания в выборку. Этот принцип обеспечивает объективность выборочного наблюдения, поскольку позволяет сформировать репрезентативную выборку. Репрезентативность способствует получению несмещённой выборки, т.е. структура или закономерность распределения в выборочной совокупности соответствует распределению единиц в генеральной совокупности.
Способы отбора единиц в выборочную совокупность:
1. Случайный отбор. Реализуют методом жеребьёвки или с использованием таблиц случайных чисел.
2. Механический отбор – частный случай случайного отбора. Рассчитывается шаг отбора, который равен отношению объёма совокупности к объёму выборки: ![]() .
.
Отбор может проводиться по принципу бесповторного отбора, когда, извлекаемая из генеральной совокупности, единица назад не возвращается, и повторного отбора [1].
Виды выборки:
1. Собственно случайная.
2. Типологическая (стратифицированная).
3. Гнездовая (серийная).
4. Многоступенчатая.
5. Многофазная.
Лабораторная работа выполнена на основе исходных данных первой лабораторной: данные сборника Росстата Регионы России [2], а именно статистическая информация о числе собственных легковых автомобилей на 1000 человек населения в различных регионах России в 1990 году. Объём исходной совокупности – 88 единиц.
1. Расчёт необходимого объёма выборочной совокупности
Ошибка выборки – это различие в значениях какого-либо параметра генеральной совокупности и его оценки, полученной на основе выборки. Ошибка выборки присутствует всегда, т.к. её возникновение связано с самой сутью выборочного наблюдения: по части судят о целом. Распределение единиц выборочной совокупности не может в полной мере соответствовать распределению единиц генеральной совокупности. Понятию ошибки выборки и методике её определения посвящены многие работы теории выборки (учёные – Я. Бернулли, П.Л. Чебышев, А.М. Ляпунов, А.А. Марков, А.А. Чупров и др.).
Теорема Чебышева. При неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией с вероятностью, близкой к единице, можно утверждать, что величина ошибки выборки не превысит сколь угодно малой положительной величины ξ.
![]()
![]() ,
,
где ![]() – выборочное среднее,
– выборочное среднее, ![]() – генеральное среднее,
– генеральное среднее, ![]() – вероятность события, заключённого в скобки.
– вероятность события, заключённого в скобки.
Теорема Чебышева доказывает принципиальную возможность оценки параметров генеральной совокупности на основе выборочных данных, утверждая, что в условиях большой выборки вероятность получить незначительную величину ошибки близка к 1. Однако, практически не ясно, чему равна эта вероятность, и какова величина ошибки выборки.
Теорема Ляпунова. При неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией вероятность того, что ошибка выборки не превысит величины tμ, равна нормированной функции Лапласа:
![]() ,
,
где μ – средняя ошибка выборки, 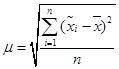 ,
, ![]() – среднее выборочное по i‑й выборке, n – число выборок.
– среднее выборочное по i‑й выборке, n – число выборок.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--