Известно, что (S² – дисперсия выборки). Если выборка большого объёма, то , следовательно, на практике сомножитель опускают и .

Предельная ошибка выборки . Плотность нормального распределения: , где нормированное отклонение выборочной средней от генеральной средней .

Данное исследование проводится с вероятностью 0,95. Этому значению в таблице Лапласа соответствует t=1,96, которое на практике округляют до 2. В этом случае . Тогда .

Важным вопросом подготовки выборочного наблюдения является определение объема выборочной совокупности, необходимой и достаточной для оценки тех или иных свойств генеральной совокупности. В практике экономико-статистических исследований, как правило, используется процедура бесповторного отбора единиц в выборочную совокупность. Первым этапом подготовки выборочного наблюдения является расчет объема выборки. Расчет, как правило, проводится по следующей формуле: [3].

Расчёт объёма выборки проводится многократно с учётом разной величины ошибки и с разным уровнем вероятности. По полученным результатам выбирают оптимальный вариант. В лабораторной работе будет сформировано три выборки, объёмом 70, 25 и 15 единиц каждая.

2. Формирование выборочных совокупностей и обработка выборочных данных

Методом случайного бесповторного отбора формируются большая (70 единиц) и две малых выборки (25 и 15 единиц). Затем, при помощи ППП Statistica рассчитываются основные статистические характеристики, данные занесены в таблицу ниже.

Таблица 2.1 . Основные статистические характеристики выборок

В таблице 2.1 «NewVar1» обозначает выборку размером 70 единиц, «NewVar2» – 25 единиц, «NewVar3» – 15 единиц. В графе «Mean» указаны значения средних по каждой выборке, «Std. Dv.» – стандартное отклонение, «N» – объём выборки, «Std. Err.» – средняя ошибка выборки, «Confidence -95,000%» и «Confidence +95,000%» – соответственно нижняя и верхняя границы доверительного интервала при вероятности 95%, «Reference» – гипотетическое значение генеральной средней величины (известно из первой лабораторной работы), «t-value» – расчетное значение t‑критерия для проверки гипотезы о значении генеральной средней, «df» – число степеней свободы, «p» – расчетный уровень значимости t‑критерия.

Среднее значение выборки, состоящей из 70 единиц, равно 53,64286, оно отличается от генеральной средней на 2,06309, величина среднеквадратического отклонения равна 16,66183. Средняя ошибка этой выборки – 1,991470, а интервал оптимальности , т.е. с вероятностью 95% можно утверждать, что в среднем по России число собственных легковых автомобилей на 1000 человек населения в 1990 году находилось в указанных пределах. Расчётное значение t-критерия составляет -1,03596, меньше 2, следовательно, различия между генеральной и выборочной средней случайны, и выборочное среднее является достоверной оценкой генеральной средней. Расчётный уровень значимости t-критерия также подтверждает это ().

3. Распространение результатов выборочного наблюдения на генеральную совокупность

Теперь необходимо провести оценку существенности разности двух выборочных средних. Если разность между средними величинами статистически значима, это означает, что различие вызвано неслучайными факторами, или выборки не принадлежат одной генеральной совокупности. Иначе эта задача формулируется как проверка статистической гипотезы о равенстве двух средних: .

В лабораторной работе содержательно гипотеза формулируется следующим образом: взяты выборки из одной или из разных генеральных совокупностей? В контексте решаемой задачи ответ очевиден – выборки взяты из одной и той же совокупности. Но следует обратить особое внимание на проявление эффекта случайной ошибки репрезентативности. Реализация процедуры проверки гипотезы может дать, в редких случаях, парадоксальный результат, а именно, показать на основе t‑критерия, что выборки как бы взяты из разных генеральных совокупностей с разными значениями средних величин. С дидактической точки зрения такой результат весьма полезен для понимания существа статистических выводов и степени их условности. Для демонстрации этого эффекта рекомендуется взять такие две выборки, из ранее полученных, для которых разность между средними выборочными значениями максимальна [3].

В данной работе для сравнения взяты выборки, объёмом 70 и 25 единиц. Результаты анализа занесены в таблицу ниже.

Таблица 3.1 . Результаты расчёта t-критерия для выборок, объёмом 70 и 25 единиц

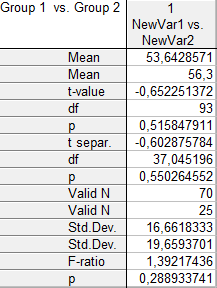
В полученной таблице рассчитаны следующие показатели:

- Mean – среднее значение по двум выборкам.

- t-value – t‑критерий, необходимый для оценки существенности разности двух средних: 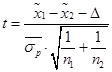, т. к. , то .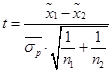

- df – число степеней свободы.

- p – расчётный уровень значимости t‑критерия.

- t-separ– расчетное значение t‑критерия с учетом различных дисперсий. Очевидно, что в этом примере оно не изменяется, однако программа выдаёт другой результат.

- df – число степеней свободы t‑критерия при условии неравных дисперсий. 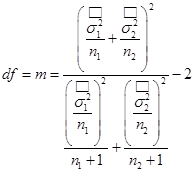. Расчетное значение mокругляется до целого значения в силу того, что число степеней свободы есть целое число по определению.

- p– расчетный уровень значимости t‑критерия при условии неизвестных и неравных дисперсий.

- ValidN – объём каждой выборки.

- Std. Dev. – среднее квадратическое отклонение: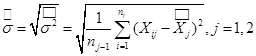

- F-ratio– F‑критерий (дисперсионное отношение), используемый для оценки существенности различия значений двух дисперсий: .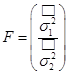

- p –расчетный уровень значимости P‑критерия.

Гипотеза принимается, если . Здесь . Табличное значение t‑критерия равно . Таким образом , следовательно, испытуемая гипотеза принимается. Аналогичный вывод можно получить на основе сравнения расчетного и принятого уровней значимости: .

4. Проверка статистических гипотез о значении генеральной средней и о равенстве двух выборочных средних

Для наглядного и компактного представления результатов проведенного выборочного наблюдения необходимо воспользоваться графическими возможностями ППП STATISTICA. Весьма существенным, с дидактической точки зрения, является то, что последовательное выполнение рассматриваемых лабораторных работ, дает возможность наглядного сравнения результатов выборочного и сплошного наблюдений. Вполне очевидно, что, по определению, такое сравнение исключено в реальных практических условиях [3].