Лабораторная работа: Расчет линейных цепей постоянного тока

Определить ток I1 в заданной по условию схеме, используя теорему об активном двухполюснике и эквивалентном генераторе

Представим всю схему в виде активного двухполюсника, у которого Е=Uadxx, а внутреннее сопротивление генератора равно входному сопротивлению двухполюсника. Для этого выделим сопротивление R1 и выберем путь от точки a к точке cи применяя закон Ома найдем разность потенциалов (напряжение) между точками a и c.

Перечертим данную схему, убрав сопротивление R1:

Так как было исключено сопротивление R1, то в схеме появились новые (частичные) токи. Значения которых можно найти, используя метод контурных токов:

R11I11+R12I22=E11

R21I11+R22I22=E22,

где

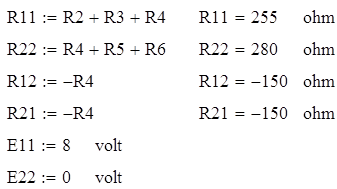
Тогда подставляя полученные значения в систему и решая ее получим следующие значения контурных токов:

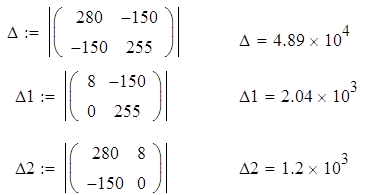
Согласно полученному результату частичные токи I2=I3=I11, I5=I6=I22. Причем данные токи будут направлены в туже сторону, что и контурные токи. Найдем напряжение между точками a и с, для этого заземлим точку а, ее потенциал будет равен нулю, и по методу узловых потенциалов найдем потенциал точки с:

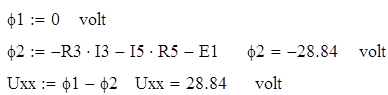
С помощью прямого преобразования (треугольника в звезду) найдем входное сопротивление двухполюсника.

Согласно расчетным формулам преобразования:

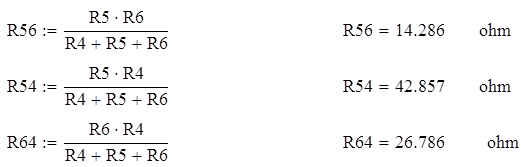
Перечертив схему согласно предыдущим преобразованиям, получим:

Согласно данному чертежу имеем смешанное соединение проводников, где резисторы R54 и R3, R64 и R2 соединены последовательно, между собой параллельно, а с резистором R56 последовательно, и их общее сопротивление равно эквивалентному и входному сопротивлению схемы относительно точек a и с. Рассчитаем входное сопротивление относительно точек a и с.

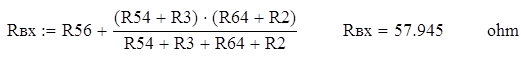
Тогда согласно расчетной формуле, ток, протекающий через первый резистор, будет равен:

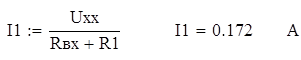
Задание №7

Начертить потенциальную диаграмму для любого замкнутого контура, включающего обе э.д.с.

Для того чтобы начертить потенциальную диаграмму для любого замкнутого контура, включающего обе э.д.с.:

1) выберем замкнутый контур acba и заземлим точку b

2) выберем направление тока в этом контуре и найдем его значение как:

Iобщ. = I =Eобщ./Rобщ. , где

Eобщ.=E=E1+E2

Rобщ.=R=R1+R2+R6