Лабораторная работа: Разложение в ряды Тейлора
Т. р. является мощным аппаратом для исследования функций и для приближённых вычислений. Пэтому данная работа посвящена именно ему.
Постановка задачи
Задача заключается в том, чтобы посчитать через ряд Тейлора функцию и сравнить её значение с значением стандартной функции в паскале.
Предлагается рассмотреть три функции: sin, cos и exp.
Для каждой из них существует разложение в ряд Тейлора.
Разложения:
1. ![]()
2. ![]()
3. ![]()
Бесконечно малыми пренебрежем.
Руководство пользователя
1. Запускаем программу.
На экране появляется главное меню:
1 – sin x
2 – cos x
3 – exp x
4 – Выход
2. Выбираем функцию: синус, косинус или экспонент.
3. Вводим аргумент.
4. Вводим количество слагаемых.
5. Получаем результат и точность в вычислении.
Примечание
Под точностью понимается количество членов ряда.

Главное меню
Руководство программиста
В программе используются переменные процедурного типа.
Точнее, мы присваиваем переменной процедуру, проверяем корректность заданного параметра и потом с помощью переменной процедурного типа вычисляем пошагово в цикле очередной член ряда и прибавляем его к сумме.
? ????????? ???????? ?????????? ????????? ?????????: ????????, ???????? ?????????? (????? ?????? ????) ? ?????????? ???????????? ????, ??????????? ?? ???????, ??????? ?????????? ????? ???? ????. ??????? ????????? ????? ???? ???? ?? ?????? ????????? ? ?????? ?????. ? ??????? ?? ?????????? ?????????? ???? ????, ????????? ????????? ?????????? ???? ??????? ??????????? ?? ?????????? ???? ????.Заключение
При большом количестве членов ряда (начиная с 10-14 для разных рядов) погрешность в вычислениях становится настолько мала, что иногда округляется до нуля. При стремлении числа слагаемых в бесконечность погрешность стремится к нулю. В результате мы получаем корректный результат при большем количестве членов ряда.
В результате данной работы была написана программа и были проведены эксперементы, результатами которых явилось:
1. 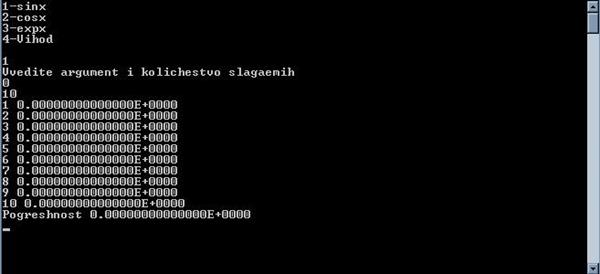
Sin x
2. Cos x
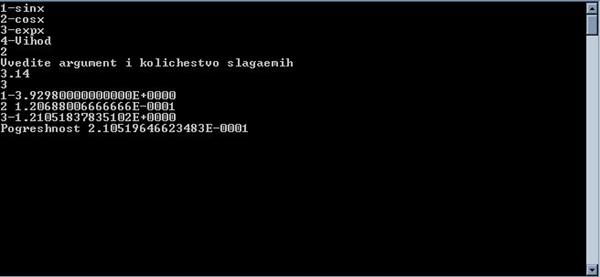
3. Exp X
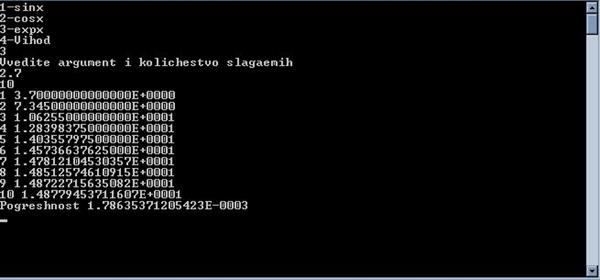
Список литературы
1. Л.Д. Кудрявцев «Курс математического анализа»
2. В.Г. Абрамов, Н.П. Трифонов, Г.Н. Трифонова «Введение в язык Паскаль».
Приложение
program teylor;
uses
SysUtils;
var a,x,sum: real;
n,i,answ: integer;
begin
writeln ('Viberite funkciyu');
writeln ('1-sinx');
writeln ('2-cosx');
writeln ('3-expx');
writeln ('4-Vihod');
readln (answ);
writeln ('Vvedite argument i kolichestvo slagaemih');
readln (x,n);
case answ of
1: begin
a:=x;
sum:=a;
for i:=1 to n do
begin
a:=a*(-1)*x*x/(2*i*(2*i+1));
sum:=sum+a;
writeln (i, sum);
end;
writeln ('Pogreshnost', abs(sin(x)-sum));
end;
2: begin
a:=1;
sum:=1;
for i:=1 to n do
begin
a:=a*(-1)*x*x/((2*i)*(2*i-1));
sum:=sum+a;
writeln (i, sum);
end;
writeln ('Pogreshnost', abs(cos(x)-sum));
end;
3: begin
a:=1;
sum:=1;
for i:=1 to n do
begin
a:=a*x/i;
sum:=sum+a;
writeln (i, sum);
end;
writeln ('Pogreshnost', abs(exp(x)-sum));
end;
end{case};
readln;
end.