Лабораторная работа: Решение уравнений, неравенств и их систем

> d-(h<4);

При проверке типа объекта, представляющего неравенство, в области вывода отображается либо <>, либо <, либо <=. Дело в том, что Maple “понимает” только эти три типа. Неравенства противоположного знака приводятся к ним перестановкой левой и правой частей с заменой знаков на противоположные.

2. Команда: solve ( )

Команда solve() позволяет решать уравнения и системы уравнений, неравенства и системы неравенств. Эта команда всегда пытается найти замкнутое решение в аналитической форме. Ее синтаксис достаточно прост:

solve (ypaвнение, переменная);

solve ({уравнение l, уравнение 2, ... }, {переменная l, переменная 2, …});

Первая форма команды предназначена для решения одного уравнения относительно заданной переменной. Вторая форма позволяет решать системы уравнений относительно переменных, заданных вторым параметром. Заметим, что система уравнений и ее неизвестные переменные задаются в виде множеств, результатом в этом случае является также множество значений неизвестных в виде уравнений. В случае задания одного уравнения результатом будет выражение (в случае одного корня уравнения) или последовательность выражений (в случае нескольких корней). Если не задана переменная/переменные, относительно которых следует решать уравнение/систему уравнений, то Maple выдаст все решения относительно всех неопределенных переменных в исходных уравнениях. Если вместо уравнения задано выражение с неизвестными, то оно рассматривается как левая часть уравнения, тогда как правая часть предполагается равной 0. Некоторые из перечисленных ситуаций иллюстрирует пример 3.

Пример 3. Решение уравнений и систем уравнений.

> a:=x^2+7*x+y^3=0;

> solve(a,x);

> solve({a},x);

> a1:=2*x+y=0;

> solve({a,a1},{x,y});

> solve(a1);

В некоторых случаях команда solve() возвращает пустую последовательность NULL. Это означает, что решения или не существует, или Maple не удалось его найти. Если не удалось найти все решения, то глобальная переменная _SolutionsMayBeLost устанавливается равной true.

Последнее уравнение из примера 3. решалось без указания переменной, относительно которой следовало бы решать уравнение. Maple решил их относительно всех неизвестных величин, входящих в уравнение. Причем он выбрал неизвестную х в качестве параметра (х = х), а неизвестную переменную у выразил через введенный параметр х. Чтобы получить решение, следует параметру х присвоить произвольное значение, тогда значение неизвестной у будет определено однозначно.

В общем случае полиномиальное уравнение степени выше 4 может не иметь решения, выраженного с помощью радикалов. В этом случае для представления результатов Maple использует специальную функцию RootOf(), которая применяется для обозначения любого корня выражения, заданного в качестве ее параметра:

> eq:=x^5+x^4+x^3+8=0;

> d:=solve(eq,x);

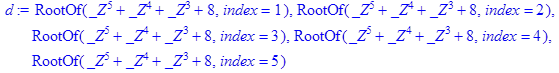
> evalf(d[1]);