Составим матрицу коэффициентов системы (5) с учетом того, что коэффициент при р_т в т-м уравнении в силу (1) равен

,

Столбцы Р

1

2

3

…

m-1

m

m+1

m+2

…

m+i

m+i+1

m+i+2

…

n-1

n

Строки

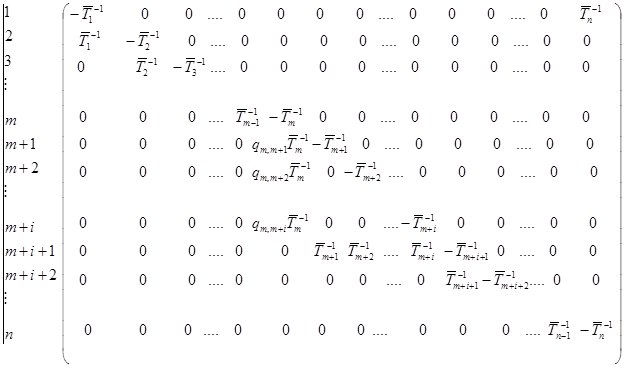
Проведем следующие элементарные преобразования над строками этой матрицы:

2-ю строку прибавим к 3-й строке;

полученную 3-ю строку прибавим к 4-й строке;

полученную 4-ю строку прибавим к 5-й строке;

и так далее;

полученную ( m -1)-ю строку прибавим к m -й строке;

полученную m -ю строку умножим последовательно на и прибавим соответственно к (m +1)-й, (m +2)-й,..., ( m + i )- йстроке;

сумму полученных (m +1)-й, (m +2)-й,..., ( m + i )- йстрок прибавим к (m + i +1)-й строке, учитывая равенство (1);

полученную (m + i +1)-ю строку прибавим к (m + i +2)-й строке;

полученную ( m + i +2) строку прибавим к (m + i +3)-й строке;

и так далее;

полученную (п -1)-ю строку прибавим к п- йстроке.

В результате этих преобразований получим матрицу следующего вида:

Первая и последняя строки этой матрицы пропорциональны, а потому одну из них, например первую, можно отбросить.

Полученная после отбрасывания 1-й строки матрица порождает следующую систему линейных уравнений:

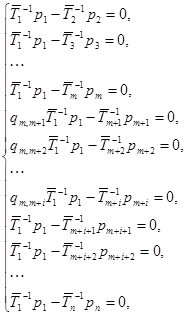
Отсюда финальные вероятности можно выразить через финальную вероятность :

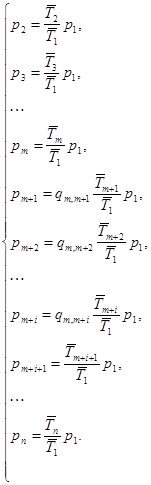(6)

Подставим выражения (6) в нормировочное условие и найдем :

.

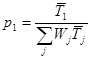Откуда или , где 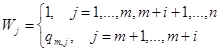. Подставляя найденное выражение в (6) получаем доказываемые формулы.

Практика

В наше время любой банк имеет банкоматы в различных точках города для удобства своих клиентов. Для планирования будущих расходов на содержание банкомата применим теорию о ветвящихся циклических процессах.

В качестве системы S возьмём банкомат. Банкомат может находиться в следующих состояниях:

S₁ – исправен, работает;

S₂ – неисправен, ведётся поиск неисправности;