Научная работа: Розвязування задач за допомогою графів

Таблиця влаштована таким чином.

У першому рядку, як вже було сказано, перераховані гравці від 1 до N; ці ж числа ми поставили і в першому стовпці. Тепер на N - 1, що залишилися, місць кожного рядка ми ставимо числа від 2 до N в циклічному порядку по вибуванню. Перші ½N рядків починаються з парних чисел 2,4..., N і виглядають так:

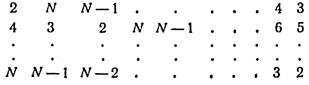
Решта рядків починається з непарних чисел 3,5..., N - 1 і мають вигляд

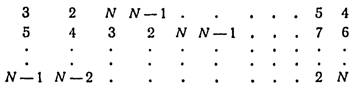
Відмітимо, що в цій таблиці відсутнє число 1; з іншого боку, оскільки ніхто не грає проти самого себе, те число, що стоїть зверху стовпця, ніколи не повинне в цьому стовпці повторюватися. Ми усунемо обидва недоліки, якщо замінимо всі числа, що стоять на головній діагоналі, одиницями, як показано на додатку 4. Тепер кожен гравець знайде під своїм номером номери гравців, з якими він грає в різних турах. Наприклад, гравець 4 грає з гравцем N - 1 в першому турі, з гравцем 2 в другому турі, з гравцем 1 в третьому турі, з гравцем 6 в четвертому турі і так далі і, нарешті, з гравцем N - 3 в (N - 1) - му турі.

Висновок: розв’язавши цю задачу, я зрозумів, що тепер організаторам спортивних змагань буде набагато простіше працювати, звісно, якщо вони прочитають подібний матеріал.

Задача про сполучення міст

Я хочу зупинитися на задачі про засоби сполучення, поставивши її спочатку формі питання про проведення доріг. Є декілька міст А, B, С,..., які потрібно з'єднати між собою мережею шосейних або залізних доріг. Для кожної пари міст A, B відома вартість с(А, B) будівництва сполучаючої їх дороги. Завдання полягає в тому, щоб побудувати найдешевшу з можливих мереж доріг. Замість того, щоб говорити про мережу залізниць, можна було б говорити про електричні лінії, або про водопроводи, або про нафтопроводи і тому подібне

B тому окремому випадку, коли є всього три міста A, B, C, досить побудувати одну із ліній АВС, АСВ, ВАС, причому, якщо ВС - найдорожча лінія, то саме її і треба виключити, побудувавши дорогу ВАС.

Розглянемо тепер загальний випадок. Граф найбільш дешевої сполучаючої мережі має бути деревом, оскільки якби він містив цикл, можна було б видалити одну з ланок цього циклу і міста все ще залишилися б сполученими. Отже, для сполучення n міст потрібно побудувати n - 1 доріг.

Ми покажемо, що мережу мінімальної вартості можна побудувати, користуючись наступним простим правилом економічності. Перш за все, сполучаємо два міста з найбільш дешевою сполучаючою ланкою S1. На кожному з наступних кроків додаємо найдешевшу з ланок S1 при приєднанні якого до вже побудованих ребер не утворюється ніякого циклу; якщо є декілька ланок однієї і тієї ж вартості, вибираємо будь-яке з них.

Кожне дерево Т, побудоване таким чином, що ми називатимемо економічним деревом. Його вартість дорівнює сумі вартостей окремих ланок:

с(Т) = с(S1) + с(S2) +... + с(Sn-1).

Нам треба довести, що жодне інше дерево В, що сполучає ті ж вершини, не може виявитись дешевше за економічне дерево Т. Нехай В - найдешевше дерево, що сполучає наші вершини, а Т - будь-яке економічне дерево. Припустимо, що ребра S1, S2... економічного дерева Т занумеровані в тому порядку, в якому вони приєднувалися при побудові Т. Якщо найдешевше дерево В не збігається з Т, то Т має щонайменше одне ребро,що не належить В. Нехай S1= (A, В) - перше таке ребро, і нехай Р(А, В) - ланцюг графа В, що сполучає вершини A і B (додаток 5).

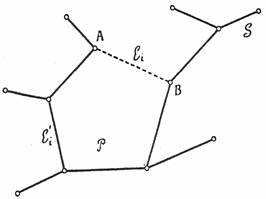
Якщо ребро S1 додати до В, то граф В+S1, міститиме цикл С= S1+Р(А, В), а оскільки Т не має циклів, то цикл С повинен містити принаймні одне ребро, що не належить Т. Видаливши це ребро S1 ми отримаємо дерево

В’=В+S1 - S1’

з тією ж кількістю вершин, що і В, причому його вартість дорівнює

C(В’) =c(В) +с(S1) - с(S1’)

Оскільки В має найменшу можливу вартість, то

с(S1) ≥с(S1’)

Але S1; було ланкою найменшої вартості, при додаванні якого до S1, S2..., Sn-1 не виходить циклів.

Оскільки при додаванні ребра S1’ до цих ребер ми теж не отримаємо ніякого циклу, то

с(S1) = с(S1’)

і, отже, В' теж має мінімальну вартість:

c(В) = c(В’).

Таким чином, ми знайшли інше дерево В’ мінімальної вартості, що має з економічним деревом Т на одне спільним ребро більше, ніж В. Ми можемо повторювати цю операцію до тих пір, поки остаточно не отримаємо сполучаюче дерево мінімальної вартості, яке співпадає з Т. Таким чином, Т, а також всі інші економічні дерева дійсно мають мінімальну вартість.

Висновок: такі задачі спростять роботу будь-якому планувальнику, допоможуть вберегти скарбницю певної держави від надлишкових витрат, знайшовши найдешевший варіант сполучення міст комунікаціями.

Знову спортивні змагання

Розв’язуючи задачу про спортивні змагання, ми об’єднували дві команди, скажімо А і C ребром АС у тому випадку, коли ці команди вже грали один з одним. Проте такий граф не дає відповіді на одне вельми суттєве питання: хто саме виграв гру?