Научная работа: Розвязування задач за допомогою графів

Якщо S - циклічне ребро, то воно входить в деякий цикл С і тоді на всіх ребрах циклу С можна встановити циклічну орієнтацію; ясно, що з будь-якої вершини G можна перейти до будь-якої іншої, прямуючи вказаним на ребрах напрямом (додаток 13).

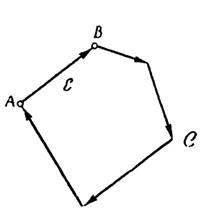
Цей процес можна продовжити. Припустимо, що ми вже орієнтували деяку частину H даного графа так, що з будь-якої вершини графа H можна пройти в будь-яку іншу його вершину з дотриманням правил одностороннього руху. Оскільки граф G є зв'язним, то або N збігається з усім графом G, або знайдеться ребро S = (А, В), що "торкається" Н, тобто таке, що воно не належить H, але одна з його вершин, скажемо A, належить Н.

Якщо S - зв'язуюче ребро АВ, то, як ми вже умовилися, воно залишається двостороннім. Тоді для будь-якої вершини X графа H можна знайти орієнтований ланцюг R, що сполучає X з A, а значить (через ребро S), і з B. Назад, від вершини B через ребро S можна перейти до A, а потім - по орієнтованому ланцюгу Z - від А до X (додаток 14).

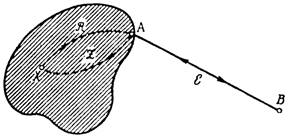
Приєднуючи S до H, ми отримаємо вже велику частину графа G, що має необхідну властивість.

Якщо ж ребро S = (А, B) є циклічним, воно належить деякому циклу С. Ми встановимо напрям на С від А до B і далі уподовж С до першої вершини D з С, що належить H (додаток 15)

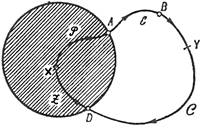
Всі ці ребра ми приєднаємо до H. Нехай X - довільна вершина з Н, а Y - будь-яка вершина із С: можна знайти орієнтований ланцюг Р, що належить Н і що сполучає Х з A, а потім уподовж С пройти до вершини Y з С. Назад від Y можна пройти уздовж С до вершини D, а від неї - належним Н, орієнтованим ланцюгом Z - від D до X. Тому орієнтований граф, отриманий додаванням до Н вказаних ребер циклу С, також задовольняє необхідні умови: те, що від будь-якої з доданих вершин циклу С можна пройти до будь-якої іншої з цих вершин з дотриманням умов, пов'язаних з орієнтацією ребер, очевидно (додаток 15), продовжуючи цей процес, ми в кінці кінців орієнтуємо необхідним чином початковий граф G.

Встановлення на вулицях міста одностороннього руху дозволяє сильно збільшити швидкість руху транспорту; проте воно ставить справжні головоломки перед водієм, який хоче об'їхати на машині незнайоме йому місто. Якщо на вулицях скрізь або частково встановлений односторонній рух, то завдання стає набагато складнішим, навіть якщо зроблено необхідне припущення про існування, принаймні одного орієнтованого ланцюга, що сполучає будь-яку пару вершин графа.

Загальна проблема така: яким способом можна рухатися по графові уздовж вказаних напрямів, щоб зрештою пройти по всіх його ребрах? Для цього, звичайно, треба мати хорошу пам'ять, а ще краще заздалегідь скласти нарис графа, утвореного мережею вулиць.

Ми відправляємося з деякої точки а0 по одній з вулиць, що виходять з неї. Проходячи перехрестя, ми позначаємо на малюнку, по якій вулиці ми сюди прийшли і на яку нову вулицю переходимо; для подальшого корисно відзначити також і інші вулиці, що виходять на це перехрестя, разом з їх напрямами. Через деякий час ми повернемося до одного з перехресть а1, на якому ми вже побували раніше (додаток 16).

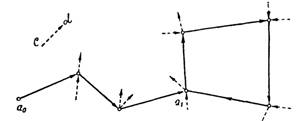
Подивимося на план, складений нами заздалегідь, якщо ми вже обійшли всі вулиці міста, то наше завдання вирішене. B протилежному випадку знайдеться ще не пройдена вулиця (с, d). По припущенню, існує орієнтований ланцюг, сполучаючий а1 з с; ми підемо по ньому, а потім пройдемо вулицю (с, d) (зрозуміло, найзручніше починати з не пройдених раніше вулиць, що виходять з а1) Ясно, що, діючи і далі так само, ми врешті-решт обійдемо всі вулиці міста.

Висновок: якщо органи міського управління приймуть до уваги результат дослідження цієї задачі, то затори зникнуть з вулиць будь-якого міста.

Висновок

В моїй роботі описувались важливі методи, які можуть допомогти розв’язати деякі життєві проблеми.

Вивчивши основи теорії графів, ознайомившись з розв’язанням класичних задач, досліджено розв’язання деяких задач за допомогою графів. Розглянуто, як можна використовувати задачі на практиці: прокладення комунікацій, розподіл посад між претендентами, складання турнірних таблиць, планування руху в містах...

Працюючи над роботою, я зрозумів, що дана тема є актуальною і перспективною в наш час.

Список використаної літератури

1. Барболин М.П. Головоломки и графы. Квант, 1975, №2

2. В.А. Носов. Комбинаторика и теория графов, МГТУ, 1999

3. Уилсон Р. Введение в теорию графов. М., Мир, 1977

4. Головина Л.И. Графы и их применения. Математика в школе, 1965,№ 3

5. Новиков Ф.А. Дискретная математика, 2001

6. Шедиви Я. Решение логических задач при помощи графов. - Математика в школе, 1967, № 6

7. Головина Л.И. і Яглом И.М., Индукция в геометрии, М., Физматгиз, 2000.

Словник термінів

Граф. Фігура, що складається з точок (вершин) і відрізків, що сполучають деякі з цих вершин. Сполучаючі відрізки можуть бути прямолінійними або криволінійними; вони називаються ребрами графа.

Дерево. Зв'язний граф, що не має циклів.

Многогранник. Тривимірне тіло, межа якого складається з плоских багатокутників.

Нульовий граф. Граф, що складається тільки з ізольованих вершин: граф, що не має ребер.