Отчет по практике: Разработка системы краткосрочного прогнозирования спроса на продукцию с использованием принципа самоорганизации

- прогноз на момент времени

- текущий момент времени

- ошибка прогноза

3. Сезонно-декомпозиционная прогностическая модель Холта-Винтера

Модель Холта-Винтера в практике прогнозирования сезонных временных рядов встречается чаще всего. Ее прогностическая точность не уступает точности других еще более сложных моделей поведения сезонно изменяющихся временных рядов (среднеабсолютная процентная ошибка по этой модели в большинстве случаев меньше 50%). Сезонно-декомпозиционная модель Холта-Винтера основана на применении метода экспоненциального взвешенного среднего. Оценка стационарно-линейного и сезонного фактора для нее производится следующим образом.

а) Оценка стационарного фактора (т.е. оценка среднеежемесячного значения независимо от времени года). Уравнение оценки стационарного фактора:

б) Оценка линейного роста вычисляется на основе модели роста Холта:

в) Оценка сезонного фактора (адаптация коэффициента сезонности). Коэффициент сезонности представляет собой отношение значения текущего наблюдения к среднестационарному значению, т.е. этот коэффициент в момент времени t равен . Определение экспоненциального взвешенного среднего текущего значения коэффициента сезонности:

г) Прогноз . При изолированной оценке трех факторов, определяющих движение процесса, прогноз на τ моментов времени вперед строится из трех элементов: суммируется оценка линейного роста и оценка стационарного фактора , и результат с учетом сезонности домножается на соответствующее значение коэффициента сезонности :

Алгоритм вычисления прогноза методом Холта-Винтера представлен на рисунке 5.

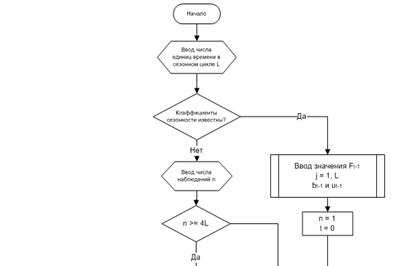
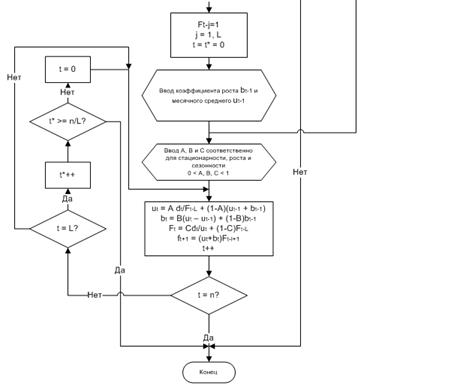
Рис.5 Блок-схема модели Холта-Винтера

4. Самоорганизующийся алгоритм прогнозирования

Процесс построения самоорганизующегося алгоритма (САП) состоит из нескольких шагов.

Шаг 1. Формирование первоначального множества простых алгоритмов прогнозирования.

На этом шаге формируется множество простых алгоритмов, которые будут использоваться при конструировании самоорганизующегося алгоритма. Под определением «простой алгоритм» мы в дальнейшем будем понимать известные алгоритмы (методы, мат. модели) прогнозирования. В первоначальное множество можно включить простые, но в тоже время, научно обоснованные статистические методы прогнозирования.

Шаг 2. Выбор критерия отбора лучшего алгоритма для формирования прогноза.

В качестве критерия отбора можно выбрать относительную или абсолютную ошибку прогнозирования, рассчитываемую в каждой точке или некоторую агрегированную ошибку за предыдущий период.

Шаг 3. Стадия обучения САП.

Проводится прогнозирование на настоящий момент (или предыдущие моменты) времени, где известно (или известны) фактические значения наблюдаемого показателя по алгоритмам из множества, сформированного на шаге 1.

Шаг 4. Оценивание качества прогноза.

Оценивание качества прогноза проводится с использованием критерия, выбранного на шаге 2. Алгоритм, показывающий минимальное значение критерия (ошибки прогнозирования), будем считать лучшим.

Шаг 5. Прогнозирование на будущий момент времени с использованием САП.

Прогнозное значение наблюдаемого показателя на следующий момент будет определяться с помощью алгоритма, отобранного на шаге 4.