Реферат: 7.Статистическое изучение вариации социально-экономических явлений
где ![]() и
и ![]() - генеральная и выборочная средняя соответственно;
- генеральная и выборочная средняя соответственно;
![]() - предельная ошибка генеральной средней.
- предельная ошибка генеральной средней.
Доверительные интервалы для генеральной доли:
![]() (1.8.3)
(1.8.3)
![]() (1.8.4)
(1.8.4)
Таблица 1.8.1
Формулы расчета ошибок выборки и основные характеристики
параметров генеральной и выборочной совокупности
| Способ отбора единиц | Характеристики | ||||
| повторный | бесповторный | объем сово-куп-ности | доля еди- ниц | средний размер приз- нака | |
| Средняя ошибка ( для средней для доли Преде-льная ошибка ( для средней для доли |
|
| Генеральная совокупность | ||
|
N |
|
| |||
| Выборочная совокупность | |||||
| n |
|
| |||
Механическая выборка применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.).
Отбор элементов осуществляется через одинаковые интервалы, шаг интервала зависит от доли выборки. Так, при ![]() = 0,05 шаг интервала составляет
= 0,05 шаг интервала составляет ![]() = 20. Ошибка механической выборки вычисляется по формуле бесповторной выборки. Для моментных наблюдений, фиксирующих состояние непрерывного процесса на определенные моменты времени, используют формулу ошибки повторной выборки.
= 20. Ошибка механической выборки вычисляется по формуле бесповторной выборки. Для моментных наблюдений, фиксирующих состояние непрерывного процесса на определенные моменты времени, используют формулу ошибки повторной выборки.
При типическом отборе генеральная совокупность разбивается на несколько типических групп по существенному признаку. При обследовании населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасль или подотрасль, форма собственности и т.п. Затем из каждой группы путем собственно-случайного или механического отбора отбираются единицы в выборочную совокупность.
При вычислении ошибки типической выборки используют среднюю из групповых дисперсий:
для средней: ![]() (1.8.5);
(1.8.5);
для доли: ![]() (1.8.6)
(1.8.6)
Средняя ошибка типической выборки определяется следующим образом:
для средней: ![]() (1.8.7);
(1.8.7);
для доли: ![]() (1.8.8)
(1.8.8)
Как правило, ![]() <
< ![]() , следовательно, ошибка типической выборки меньше, чем механической или простой случайной. Чаще всего используют отбор, пропорциональный численности составляющих совокупности, т. е. доля выборки для всех составляющих одинакова.
, следовательно, ошибка типической выборки меньше, чем механической или простой случайной. Чаще всего используют отбор, пропорциональный численности составляющих совокупности, т. е. доля выборки для всех составляющих одинакова.
Серийный отбор удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться районы, поселки, фирмы, акционерные общества, студенческие группы, бригады, а также упаковки с определенным количеством готовой продукции, партии товара и т.д. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:
![]() - повторный отбор (1.8.9);
- повторный отбор (1.8.9);
![]() - бесповторный отбор (1.8.10),
- бесповторный отбор (1.8.10),
где r – число отобранных серий;
R – общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:
![]() (1.8.11),
(1.8.11),
где ![]() - средняя i -й серии;
- средняя i -й серии;
![]() - общая средняя по всей выборочной совокупности.
- общая средняя по всей выборочной совокупности.
При серийном отборе ошибка будет меньше, чем при механическом отборе.
Многоступенчатая выборка предполагает извлечение из генеральной совокупности сначала укрупненных групп единиц, затем групп, меньших по объему, и так до тех пор, пока не будут отобраны те группы (серии) или отдельные единицы, которые будут подвергнуты наблюдению. Выборка может быть двухступенчатой, когда генеральная совокупность разбивается на группы и производится отбор групп, а затем внутри групп – отбор единиц наблюдения. На обеих ступенях отбор может вестись в случайном порядке. В этом случае ошибка рассчитывается следующим образом:
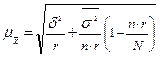 (1.8.12)
(1.8.12)
В отличие от типического отбора, где отбор производится из всех без исключения групп, при многоступенчатом отборе производится отбор самих групп, и, следовательно, не все они попадают в выборку.
Число ступеней отбора может быть и более трех. Если число ступеней отбора больше двух, то средняя ошибка выборки определяется по формуле:
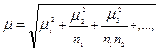 (1.8.13)
(1.8.13)
где ![]() ,
, ![]() ,
, ![]() - средние ошибки выборки на отдельных ступенях отбора;
- средние ошибки выборки на отдельных ступенях отбора;
![]() - численность выборок на соответствующих ступенях.
- численность выборок на соответствующих ступенях.
Многофазная выборка отличается от многоступенчатой тем, что на каждой стадии сохраняется одна и та же единица отбора, но изменяется программа наблюдения. Причем расширенная программа обязательно содержит вопросы краткой программы, что делает возможным проверить репрезентативность выборки. Расчет ошибки многофазной выборки производится для каждой фазы в отдельности.
1.8.3 Определение необходимого объема выборки
В практике проектирования выборочного наблюдения возникает вопрос о необходимой численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик – средней и доли. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и, наконец, на базе способа отбора.
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки.