Реферат: Адсорбция и адсобционные равновесия

.

Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения, записанного в линейной форме;

, т.е. уравнение типа y = b + ax .

Такая линейная зависимость позволяет графически определить А _¥ и К . Зная А _¥ , можно определить удельную поверхность адсорбента (поверхность единицы массы адсорбента):

,

где А _¥ - предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента;

N_A – число Авогадро;

w₀ – площадь, занимаемая одной молекулой адсорбата.

1. Если с- 0, тогда уравнение примет вид:

А=А _¥ Кс ; ; А = К_г с, q =Кс ,

т.е. при с- 0 уравнение Ленгмюра переходит в уравнение Генри.

2. Если с-¥, тогда А = А _¥ , А/А _¥ = 1. Это случай предельной адсорбции.

3. Пусть адсорбция идет из смеси компонентов, в этом случае уравнение Ленгмюра записывается следующим образом:

_.

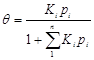Все рассмотренные выше уравнения справедливы для мономолекулярной адсорбции на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности этим свойством не обладают. Приближенной к реальности является возможность распределения адсорбционных центров по энергии. Приняв линейное распределение, Темкин использовал формулу уравнения Ленгмюра и получил уравнение для средних степеней заполнения адсорбента.

,

где  - константа, характеризующая линейное распределение;

К ₀ - константа уравнения Ленгмюра, отвечающая максимальной теплоте адсорбции.

Из уравнения следует, что увеличение парциального давления (из-за увеличения концентрации) одного компонента подавляет адсорбцию другого и тем сильнее, чем больше его адсорбционная константа равновесия. Уравнение часто называют логарифмической изотермой адсорбции. Если принять экспоненциальное распределение центров по поверхности, то в области средних заполнений получается ранее найденное эмпирическим путем уравнение Фрейндлиха :

.

Прологарифмировав, получим ,

где K , n – постоянные.

Использование уравнения Фрейндлиха в логарифмической форме позволяет определить константу уравнения.

Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.

Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию (рис. 2.3.1.2 и 2.3.1.3).

В результате этих представлений была выведена следующая формула:

- уравнение полимолекулярной адсорбции БЭТ ,

где ;

K_L = a _ж /а_п – константа конденсации пара;