Реферат: Алгебра матриц

.

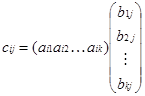Произведение С=АВ определено, если число столбцов матрицы А равно числу строк матрицы В. Это условие, а также размеры матриц можно представить схемой:

Очевидно, что операция умножения квадратных матриц всегда определена.

Примеры. Найдем произведения матриц АВ и ВА, если они существуют.

1. , .

2. , .

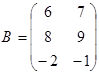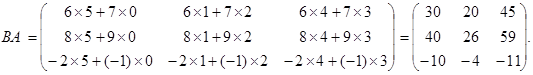
Таким образом, коммутативный (переместительный) закон умножения матриц, вообще говоря, не выполняется, т.е. В частном случае коммутативным законом обладает произведение любой квадратной матрицы А n-го порядка на единичную матрицу Е такого же порядка, т.е.

3. , .

Для этих матриц произведение как АВ ,так и ВА не существует.

,

Получим , ВА – не существует.

Свойства умножения матриц.

Пусть А,В,С – матрицы соответствующих размеров (т.е. произведения матриц определены), l - действительное число. Тогда на основании определений операций и свойств действительных чисел имеют место следующие свойства:

(АВ)С = А(ВС) – ассоциативность.

(А+В)С = АС+ВС – дистрибутивность.

А(В+С) = АВ+АС – дистрибутивность.

l(АВ) = (lА)В = А(lВ).

ЕА = АЕ = А, для квадратных матриц единичная матрица Е играет роль единицы.

Приведем пример доказательства лишь одного свойства. Докажем, например, свойство 3.

Пусть для А=(а_ij ), B=(b_ij ), C=(c_ij ) произведения матриц определены. Найдем элемент i-ой строки и j-го столбца матрицы А(В+С). Это будет число

а_{i 1} (b_{1 j} +c_{1 j} )+ а_{i 2} (b_{2 j} +c_{2 j} )+…+а_in (b_nj +c_nj ) =

(а_{i 1} b_{1 j} +a_{i 2} b_{2 j} +…+a_in b_nj )+ (а_{i 1} c_{1 j} +a_{i 2} c_{2 j} +…+a_in c_nj ).