Реферат: Алгоритм фильтрации, пример на основе БПФ

в примере 2. Ввод исходных данных аналогичен примеру 2, за исключением того, что значение I 9=0.

4. АЛГОРИТМ БПФ С ПРОРЕЖИВАНИЕМ ПО ЧАСТОТЕ

Рассматриваемый ниже алгоритм вычисления ДПФ (1.1) отличается тем, что входная последовательность х(пТ), п=0,. .., N -1, разбивается на две последовательности посередине (т. е. одна последовательность для n=0...N/2-1, а другая - для п=N/2...N -1) и эта процедура продолжается для каждой новой последовательности до тех пор, пока не получается искомая выходная одноэлементная последовательность Х (k); при этом величины Х (k) уже оказываются в выходном массиве в «прореженном» порядке и их приведение к естественному порядку связано с инверсией двоичного представления индексов k в вычисленных значениях Х (k).

Итак, запишем ДПФ (1.1) в виде:

(4.1)

Учитывая, что = получаем

. (4.2)

Подставив вместо k в (4.2) значение 2k или (2k+ 1), получим выражения для четных и нечетных отсчетов ДПФ: .

; (4.3)

, (4.4)

где теперь для значений:

Х₀ (п)=х(п) +x(n+N/2); (4.5)

Х₁ (п)=х(п) -х(n+N/2). (4.6)

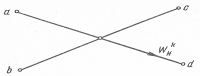
Рисунок 5 - Выполнениебазовой операции «бабочка»

Следовательно, вычисление N- точечного ДПФ X(k) сводится к вычислению двух N/2-точечных ДПФ причетных и нечетных значениях k для функций х₀ (п) и x₁ (п) и выполнениюбазовой операции «бабочка» (рис.5)отличие операции «бабочка» здесьзаключается в том, что комплексноеумножение выполняется после операции сложения-вычитания.

Ту же процедуру можно теперь применить к x₀ (п) и х ₁ (п) и перейти от N/2-точечных ДПФ к N/4-точечным ДПФ и, такимобразом, свести вычисление Х (2k) и Х (2k + 1) через Х (4k), X(4k+2), X(4k+ 1), X(4k+3). Продолжив этот процесс, перейдем в конечном итоге к 2-точечным ДП Ф с последующим прямым вычислением всех выходных отсчетов Х (k). Полный алгоритм БПФ с прореживанием по частоте и его программная реализация аналогичны рассмотренным выше для метода БПФ с прореживанием по времени.

Необходимо отметить, что в обоих алгоритмах БПФ - и с прореживанием по времени, и с прореживанием по частоте требуется примерно N log₂ N операций (комплексных умножений) и оба алгоритма могут быть реализованы по способу с замещением, используя только один массив ячеек памяти. В обоих алгоритмах должна быть предусмотрена процедура двоичной инверсии - на входе (при прореживании по времени) или на выходе (при прореживании по частоте).

5. ПРИМЕНЕНИЕ МЕТОДА БПФ ДЛЯ ВЫЧИСЛЕНИЯ ОБРАТНОГО ДПФ (ОДПФ)

По определению (1.2) ОДПФ х(пТ) N -точечной последовательности X(k), k=0, 1,..., N-1, выражается соотношением

(5.1)

причем в общем случае и х(пТ), и Х(k)-комплексные. Пусть х(пТ) и Х^* (k)-последовательности, комплексно сопряженные соответственно с х(пТ) и X(k). Согласно (5.1) можно записать

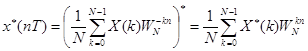(5.2)

Но выражение суммы в правой части (5.2) есть прямое ДПФ последовательности Х^* (k), k=0,. .., N-1, и, следовательно, эта сумма может быть вычислена при помощи рассмотренных алгоритмов и программ БПФ.

Таким образом обеспечивается вычисление последовательности Nx^* (пТ) и для определения х(пТ) остается взять комплексно сопряженное с Nx^* (пТ) выражение и разделить его на N:

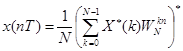(5.3)

6. ПРИМЕНЕНИЕ БПФ ДЛЯ ВЫЧИСЛЕНИЯ РЕАКЦИИ ЦФ

Вычисление реакции у(пТ) ЦФ с импульсной характеристикой h(пТ), п=0, 1,..., N-1, на входное воздействие х(пТ), п=О, 1,...M -1, может быть выполнено на основе алгоритма свертки

(6.1)