Реферат: Алгоритм фильтрации, пример на основе БПФ

для входной последовательности

(7.5)

n₁ .=0,...., N₁ -1; п₂ =0,. .., N₂ -1;

для выходной последовательности

(k₁ N₂ +k₂ )=X((s₁ k₂ N₁ + s₂ k₁ N₂ )mod N), (7.6)

k₁ =0,..., N₁ -1; k₂ =0,..., N₂ -1,

где запись п mod N означает «остаток от деления п на N», а s₁ и s₂ определяются из следующих уравнений в соответствии с китайской теоремой об остатках о восстановлении целого числа по его вычетам: s₁ N₁ = 1mod N₂ , s₁ <N₂ , s₂ N₂ == 1modN₁ , s₂ <N₁ . Тогда алгоритм N=N₁ N₂ - точечного ДПФ представляется в виде

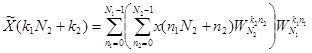Таким образом, алгоритм простых множителей (АПМ) является способом представления одномерного ДПФ в виде многомерного, причем размерность зависит от числа взаимно простых сомножителей N. Алгоритм простых множителей имеет ступенчатую форму объединения мало точечных преобразований. В данном случае на первой ступени производится N ₁ N ₂ -точечных ДПФ, а на второй ступени - N₂ N₁ -точечных ДПФ.

Впервые АПМ был предложен Гудом [3]. В том случае, когда используемые мало точечные алгоритмы синтезированы оптимальным образом по методу Винограда, получается алгоритм Гуда - Винограда [3]. Оптимальные мало точечные алгоритмы БПФ синтезируются путем сведения мало точечного ДПФ к совокупности циклических сверток. Для последних Виноградом [2] доказана теорема о существовании алгоритма вычисления с минимальным количеством умножений и был предложен метод синтеза, основанный на последовательном вычислении полиномиальных вычетов по неприводимым полиномам в поле рациональных чисел в соответствии с полиномиальным вариантом китайской теоремы об остатках [3].

7.3 Алгоритм Винограда

Дальнейшей экономии вычислений в случае разложения N на взаимно простые множители можно достичь, если ступенчатый характер объединения частичных мало точечных преобразований заменить вложенным. В этом и заключается идея алгоритма Винограда. Идею вложения мало точечных алгоритмов легче всего понять на примере.

Пример 5. Рассмотрим случай 6-точечного ДПФ, т. е. N=6. Пусть N₁ =2, N₂ =3. Приведем сначала алгоритмы мало точечных (2- и 3-точечных) ДПФ, синтезированные оптимальным образом по методу Винограда.

Алгоритм 2-точечного ДПФ

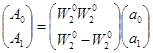
имеет вид

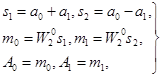(7.8)

где s_i -сложения, m_i -умножения; А_i и a_i - выходные и входные числа.

Алгоритм 3-точечного ДПФ

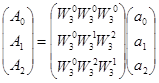
Имеет вид

, ,

, , (7.9)

, ,

Преобразуем исходную 6-точечную последовательность в двумерную точечную в соответствии с (7.5) и (7.6). Тогда матрицу 6-точечного ДПФ можно представить в виде прямого произведения 2- и 3-точечных ДПФ и преобразование можно записать в виде:

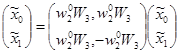, (7.10)

, , , ,

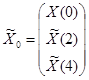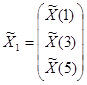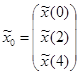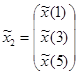Где

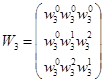
Применим к матричному преобразованию (7.10) алгоритм 2-точечного БПФ (7.8). В результате найдем векторыи :