Реферат: Анализ динамического поведения механической системы

Теперь возможную работу сил инерции можно преобразовать к виду:

(3)

Далее подставляя выражения (2) и (3) в (1), т.е в общее уравнение динамики получаем

Поделив это уравнение на , получим дифференциальное уравнение вынужденных колебаний системы:

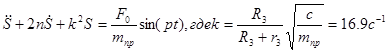
Анализ результатов

В данной курсовой работе мы исследовали динамическое поведение механической системы с использованием основных теорем и уравнений теоретической механики. Дифференциальное уравнение движения механической системы получено тремя способами. Во всех случаях коэффициенты , n, k получились одинаковыми и совпали с компьютерной распечаткой, что говорит об их правильности. В процессе решения дифференциального уравнения данной механической системы были получены законы движения первого груза, его скорость и ускорение в зависимости от времени t. На основании этих зависимостей были определены законы изменения всех остальных характеристик механической системы, в том числе и реакции связей.