Реферат: Аналіз експериментальних даних

Якщо змінна величина у змінюється в залежності від іншої змінної х, але на зміну у впливає багато інших факторів, врахувати які інколи не в змозі, то тоді кожному значенню х відповідає декілька значень у. Такі зв’зки називаються кореляційними, або зв’язок між змінними величинами х і у називається кореляційним, якщо різним значенням однієї із них (х) відповідають групові середні другої (у) або навпаки. В таких випадках одна величина розглядається як незалежна змінна і називається аргументом (х), а друга – залежна змінна і називається функцією (у). Загальний вигляд рівняння кореляційного зв’язку y=f(x), де х - аргумент, у – функція.

При графічному зображенні статистичного звя’зку часто точки розміщують так, що можна провести ряд ліній різноманітного типу.

Після встановлення форми зв’язку і її типу визначають її тісноту. В якості числового показника зв’язку простої лінійної кореляції використовують коефіцієнт кореляції

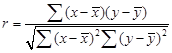(5)

де і - відхилення значень х і у від своїх середніх і в п порівнювальних парах.

Стандартну похибку коефіцієнта кореляції визначають з рівняння

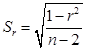(6)

r – коефіцієнт кореляції; п – число пар значень, за якими обчислений коефіцієнт кореляції. Значення коефіцієнта кореляції записується разом з його похибкою у вигляді . Критерій суттєвого коефіцієнта кореляції t обчислюють з рівняння

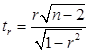або (7)

Зіставлення фактичного і теоретичного (табличного) значень t при числі ступеню волі п-2 дає можливість оцінити суттєвість r при тому чи іншому рівню значущості.

Якщо , то кореляційний зв’язок існує, а якщо - не існує.

Поряд з коефіцієнтом кореляції для характеристики зв’язку між двома ознаками використовують коефіцієнт детермінації , який чисельно рівний квадрату коефіцієнта кореляції:

(8)

Коефіцієнт детермінації показує частину тих змін, які у залежності, яку вивчають обумовлені факторіальними ознаками і дають більш чітке уявлення про ступінь спряження ознак. Наприклад, якщо коефіцієнт кореляції рівний 0,20 – 0,30, то коефіцієнт детермінації тобто тільки 4-9% всіх вимірів однієї ознаки пов’язані із змінами другої. При число зв’язків збільшується до 25-30% і тільки при біля 97% зміна результативної ознаки пов’язано із змінами факторіального.

Кореляційне відношення обчислюється

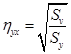(9)

де η – кореляційне відношення; S_v – сума квадратів відхилення за варіантами;

S_y – загальна сума квадратів.

Кореляційне відношення використовується для оцінки криволінійної форми зв’зку між ознаками і має додатній знак, змінюється від 0 до 1.

При малому числі спостережень кореляційне відношення обчислюється:

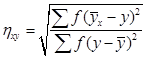(10)

де - сума квадратів відхилень групових і середніх від загальної середньої (групове варіювання), яка характеризує ту частину варіювання ознаки , яка пов’язана з мінливістю ознаки .

- сума квадратів різниці між кожним значенням і загальною середньою , яка характеризує загальне варіювання ознаки .

Похибка і критерій істотного кореляційного відношення обчислюється за рівнянням:

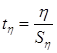; (11)

Фактичне значення порівнюють з теоретичним, який приймається для вибраного рівня значущості при числі ступенів волі з таблиці. Якщо , то кореляційне відношення суттєве.

Квадрат кореляційного відношення називають індексом детермінації:

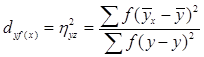(12)

Він показує ту долю варіювання ознаки , яка обумовлена змінами ознаки .