5. Фактичне значення порівнюється з теоретичним , яке приймається рівним: 8-9 ступенів волі (при - це 10-11 пар спостережень) – 2,3; для 10-14 ступенів волі – 2,2; для 15-24 ступенів волі – 2,1; для 25-100 ступенів волі – 2,0. Кореляція і регресія визначається суттєвою, якщо . В нашому прикладі , так як . Значить між вологістю грунту і її налипання є суттєвий прямий зв’язок.

6. За отриманим рівнянням регресії обчислюють теоретичне значення для крайніх величин (19,9 і 76,6, згідно таблиці)

;

Знайдені точки ( і) наносяться на графіці, з’єднуючи їх прямою, маємо теоретичну лінію регресії. Вона показує, що збільшення вологості грунту на 1% відповідає збільшенню налипання на 0,13 г/см² .

3. Парна регресія

Парна залежність може бути апроксимована прямою лінією, параболою, гіперболою, логарифмічною, степеневою або показниковою функцією,поліномом і інше.

Рис. Вигляди основних ліній різних зв’язків між змінними величинами і їх рівняння.

1. Пряма, яка проходить через початок координат має рівняння (3,а).

2. Пряма, що не проходить через початок координат має рівняння , або . Ці залежності вимагають визначення двох параметрів і . (3, б, в).

3. Парабола з вершиною в початку координат і симетрична одній із осей має рівняння . Формула один параметр із зменшенням якого зменшується розхил параболи (рис.3, г).

4. Парабола, симетрична прямій паралельній осі має рівняння . Функція квадратична. У формулі необхідно визначити три параметра: , і (рис.3, д, є).

5. Гіпербола, асимптотично наближається до осей координат, рівняння має вигляд , необхідно визначити параметр (рис.3, ж).

6. Гіпербола асимптотично наближається до прямих, паралельних до осей координат, рівняння має вигляд . Параметри і є координатами точки . Знак параметра залежить від розміщення гіперболи по відношенню до асимптот (рис.3, з).

7. Степеневі криві (рис.3, и, к), рівняння , де може бути додатнім, цілим або дробовим.

8. Показникові крива, коли із зростанням однієї величини спостерігається підсилене зростання . Рівняння (рис.8.3, л).

Двох факторне поле можна апроксимувати, площиною, параболоїдом другого порядку, гіперболоїдом. Для - змінних фактів зв’язок можна встановити за допомогою - мірного простору рівняннями другого порядку

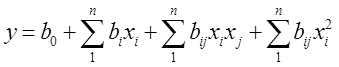(17)

де - функція мети багатофакторних змінних;

- незалежні фактори;

- коефіцієнт регресії, що характеризують вплив фактора на функцію мети;

- коефіцієнти, які характеризують подвійний вплив факторів і на функцію мети.

При побудові теоретичної регресійної залежності, оптимальною буде така функція, в якій виконуються умови найменших квадратів , де - фактичні координати поля; - середнє значення ординати з абсцисою , обчисленою з рівняння. Після кореляції апроксимують рівнянням прямої. Лінію регресії розраховують з умови найменших квадратів:

(18)

При цьому крива АВ найкращим чином вирівнює значення постійних коефіцієнтів і , тобто коефіцієнтів рівняння регресії. Їх обчислюють за формулами:

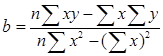(19)

(20)

Критерієм близькості кореляційної залежності між і до лінійної функціональної залежності є коефіцієнт парної або просто коефіцієнт кореляції . Він просто показує ступінь лінійності зв’язку і .

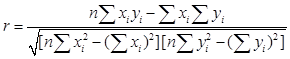(21)