Реферат: Анализ качества САУ при случайных воздействиях и их оптимизация
Значения интеграла от спектральной плотности вычислим через коэффициенты полиномов выражения для спектральной плотности.
Величина средней квадратичной ошибки -e определяется по формуле:
 .
.
 |
?????? 2. ??? ??????? ??????????? ?? ???.3 ?????????? ???????????? ????????? ??????, ????????? ????????? ?????? -z(t) ?? ???????????? ??????????
|
Рис. 3
Решение: Спектральная плотность ошибки определяется из соотношений:

Статистическая оптимизация систем управления
При статистических исследованиях систем решаются задачи оптимизации, т.е. определение систем наилучших в определенном смысле (по точности, быстродействию, надежности и т.д.).
Оптимальной системой называют систему, обеспечивающую экстремум некоторого функционала, называемого критерием оптимальности.
При статистической оптимизации систем решаются следующие задачи:
Задача анализа.
Задача синтеза.
Задача анализа
Формулировка задачи
Дано: система с заданной структурой; статистические характеристики полезного сигнала x(t) и помехи z(t).
 |
??????????: ????????? ???????, ?????????????? ??????????? ???????? ??????? ???????????? ??????.
Рис.4
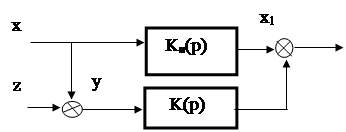
Схему исследуемой системы можно представить в виде, показанном на рис.1. При этом Ки(р) – передаточная функция идеальной системы, которая определяет закон преобразования полезного сигнала.
В системах, находящихся под действием случайного (или регулярного) входного сигнала и помехи возникает задача отделения сигнала от помехи и подавления (фильтрации) помехи. Кроме фильтрации в зависимости от оператора Ки(р) задача фильтрации сочетается с задачами:
1. Ки(р) = const – это задача воспроизведения, т.е. отделения полезного сигнала от помехи. Эта задача чаще всего используется для следящих систем.
2. Ки(р) = L(p) –задача преобразования и фильтрации. При этом L(p)- оператор преобразования.
Алгоритм решения задачи
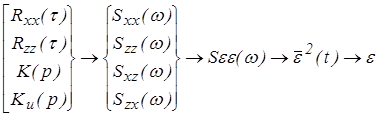 . (6)
. (6)
Величина средней квадратичной ошибки определяется по формуле:
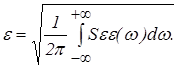 (7)
(7)
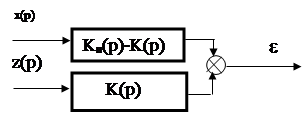 |
????? ??????????? ??????? ????? ??????????? ? ????, ?????????? ?? ???.2.
Рис. 5
Изображение ошибки равно:
![]() (7)
(7)
Спектральная плотность ошибки равна:
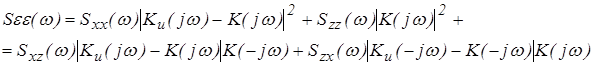 |
Если сигналы не коррелированны то