Реферат: Анализ линейной динамической цепи

Числитель:

Подставим все значения в формулу и поделим на p:

H₄₁ (p)=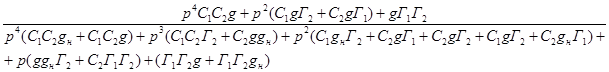

Преобразуем обратно Г₁ =1/L₁ и Г₂ =1/L₂

Подставим все значения элементов в формулу H₄₁ (p),получаем:

Перейдем к нормированной частоте:

Для проверки и для того, чтобы удостовериться, что расчеты методом обобщенных чисел верны, воспользуемся результатом, полученным при использовании программы GeneralNumbers.vi

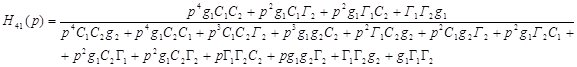
где .

Как мы видим, функция передачи, полученная методом обобщенных чисел, полностью совпадает с функцией передачи, рассчитанной с помощью программы GeneralNumbers.vi.

3. Карта полюсов и нулей

По ранее найденной комплексной функции передачи цепи определим полюса и нули:

Для нахождения нулей выпишем отдельно числитель функции и приравняем его к нулю. Корни данного уравнения и будут являться нулями.

=0

Решая данное уравнение, получим:

p_1,2,3,4 =

Для нахождения полюсов выпишем отдельно знаменатель функции и приравняем его к нулю. Корни данного полинома и будут являться полюсами.

Решив данное уравнение, мы получили полюса:

p_1,2 =-0.47751.3610j

p_3,4 =-0.22960.6542j

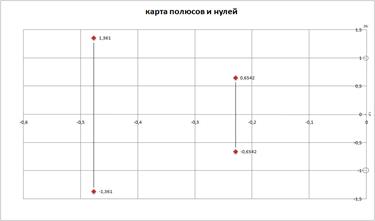
Рис 3. Карта полюсов и нулей.

По полученным значениям построим карту полюсов и нулей:

По виду карты полюсов и нулей можно определить некоторые особенности цепи:

1. Цепь является минимально-фазовой, т.к. в правой полуплоскости отсутствуют нули.