Реферат: Аналіз структурних властивостей зображень

Рисунок 2 – Одиничний імпульс

Дельта-функція має важливу фільтруючу властивість: якщо дельта-функція знаходиться під інтегралом як множник, то результат інтегрування дорівнюватиме значенню іншої підінтегральної функції в тій точці, де зосереджений дельта-імпульс:

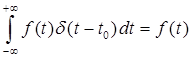. (4)

Нарешті, двовимірний дискретний сигнал (або масив, послідовність) – це функція, визначена на безлічі упорядкованих пар цілих чисел. Окремі елементи цього масиву називаються відліками. Значення відліків можуть бути речовинними або комплексними. Відповідно до визначення, двовимірні послідовності мають нескінченну довжину. Однак на практиці для більшості двовимірних послідовностей значення відліків відомі тільки в кінцевій області площини. Тому звичайно вважають, що всі значення відліків за межами визначеної області дорівнюють нулю. Приклади двовимірних дискретних послідовностей різних типів показані на рис. 3 – 6.

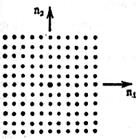
Рисунок 3 – Двовимірна одинична імпульсна функція

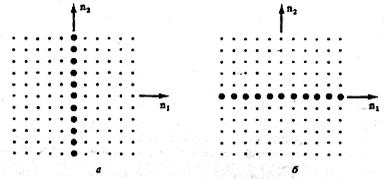
Рисунок 4 – Два приклади двовимірних лінійних імпульсів

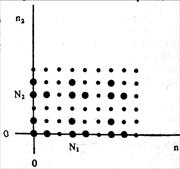
Рисунок 5 – Двовимірна періодична послідовність

Класифікація систем можлива з тих же позицій, що і класифікація сигналів:

безперервні системи —> аналогові системи:

дискретні системи —> цифрові системи.

У процесі вивчення системи досліджуватимемо орієнтовану на вирішення прикладних задач математичну модель з декількома входами і виходами, що служить для опису визначених процесів передачі сигналів від входів до виходів. Зв'язок між сигналами на входах і виходах описується за допомогою характеристик системи (рис. 7).

Рисунок 6 – Періодична послідовність

Тут послідовність x(t) є сукупністю вхідних даних, y(t) – сукупністю вихідних даних, а зв'язок між ними встановлює так звана перехідна характеристика g(t): .

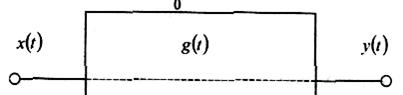
Рисунок 7 – Приклад системи

У загальному випадку вхідні і вихідні сигнали подають у вигляді векторів:

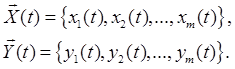(5)

Система обробки сигналів, що має m входів і n виходів називається багатовимірною. Якщо вхідний і вихідний сигнали, а також стан системи визначені в кожний момент часу і час безперервний, то система називається безперервною. Якщо згадані сигнали і стани визначено в дискретні моменти часу, система називається дискретною.

Обмежимося лінійними системами. Для розгляду лінійних процедур може бути використаний простий математичний апарат, водночас їх достатньо для опису багатьох використовуваних алгоритмів обробки сигналів.

Згортка.Нехай на вхід системи поданий дельта-імпульс, а поводження системи описується перехідною характеристикою h. Тоді на виході отримаємо імпульсний відгук системи (рис. 8):

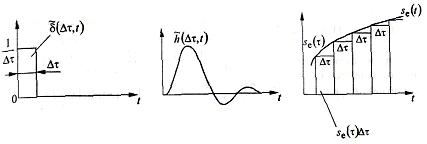
Рисунок 8 – Імпульсний відгук і постановка задачі про згортку

У процесі квантування, при , сума переходить в інтеграл, а h стає відгуком на d-імпульс. Вираз для інтеграла згортки набуває вигляду

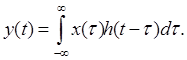(6)

Символічно згортка записується у такому вигляді: