Реферат: Анализ вариации производительности труда при производстве зерна

3. Среднегодовой темп роста:

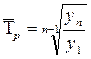100%=103,2%

4. Среднегодовой темп прироста:

=103,2%-100%= 3,2%

Согласно полученным расчетам, среднее значение трудоемкости зерна за рассматриваемый период составляет 0,5 чел.-ч. В течение десяти лет трудоемкость зерна в среднем сократилась на 0,125 чел.-ч. в год. Это явление наглядно отражает диаграмма на рис. 2.1.

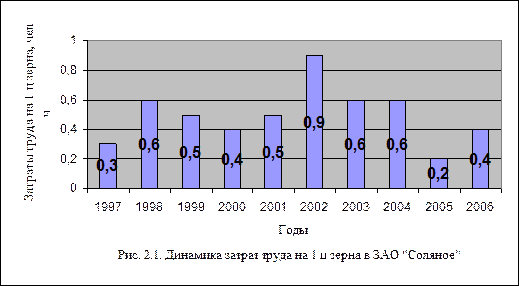
Согласно диаграмме максимального значения затраты труда на 1 ц зерна достигли в 2002 году – 0,9 чел.-ч, минимального – в 2005 году – 0,2 чел.-ч.

Исходные данные и расчеты для аналитического выравнивания ряда трудоемкости зерна приведены в таблице 2.2.

Таблица 2.2.

Выявление тенденции изменения затрат труда на 1 ц зерна в ЗАО «Соляное» за 1997-2006 гг.

Годы	Затраты труда на 1 ц. зерна, чел.-ч.	Условное время	Квадрат	Произведение	Расчетные Значения
Символы	y	t	t2	yt	y =0,5-0,0012t
1997	0,30	-9	81	-2,70	0,51
1998	0,60	-7	49	-4,20	0,51
1999	0,50	-5	25	-2,50	0,51
2000	0,40	-3	9	-1,20	0,50
2001	0,50	-1	1	-0,50	0,50
2002	0,90	1	1	0,90	0,50
2003	0,60	3	9	1,80	0,50
2004	0,60	5	25	3,00	0,49
2005	0,20	7	49	1,40	0,49
2006	0,40	9	81	3,60	0,49
Итого	5,00	0	330	-0,40	5,00

= 0,5

= -0,0012

Подставив рассчитанные параметры в уравнение прямой получим следующее уравнение:

= 0,5+ (-0,0012) t

Согласно уравнению можно сделать вывод о том, что наблюдается тенденция к снижению затрат труда на производство 1ц. зерна в среднем на 0,0012 чел.-час. (а₁ ). В среднем затраты труда на производство 1ц. зерна составляют 0,5 чел.-час (а₀ ).

На основании данного уравнения строится прямая выровненного рядя трудоемкости зерна, которая графически представлена на рис.2.2.

Из графика видно, что полученная прямая отражает тенденцию равномерного незначительного снижения трудоемкости зерна в хозяйстве за данный период.

Глава 3. Анализ вариации производительности труда при производстве зерна по 10 хозяйствам Омской области

Теперь проведем вариационный анализ. Он необходим, так как позволяет охарактеризовать совокупность одним показателем – средним значением признака, и кроме этого, показать, как распределяются около нее варианты определенного признака, то есть охарактеризовать отклонение значений от общей средней.

Средняя находится путем взвешивания индивидуальных значений признака (x) соответствующими им частотами (f):

(10)

Среднее абсолютное отклонение равно средней арифметической из абсолютных отклонений значений признака всех единиц совокупности от средней арифметической:

Средняя не показывает, как распределяются вокруг нее варианты осредненного признака, поэтому необходимо рассчитать показатели вариации, которые характеризуют отклонение значений от общей средней.

В статистике чаще всего применяются следующие показатели вариации:

1. Размах вариации – показывает крайние отклонения признака и рассчитывается как разница между максимальным и минимальным значениями:

(11)

2. Среднее линейное отклонение равно средней арифметической из абсолютных отклонений отдельных значений признака всех единиц совокупности от общей средней арифметической. Для определения среднего линейного отклонения берутся значения отклонения по абсолютной величине без учета знака этих отклонений:

- Среднее линейное отклонение: ( 12)

- Средняя арифметическая взвешенная: (13)

3. Дисперсия – средняя арифметическая квадратов отклонений каждого значения признака от общей средней

- Простая дисперсия:, (14), где